Understanding Recursion
June 11, 2012Making tree from traversals
June 12, 2012Basic Tree Traversals (Preorder, Inorder, Postorder)
If the node of a Binary tree is defined as below:
struct Node{
Node * lptr; // Pointer to Left subtree
int data;
Node *rptr; // Pointer to Right subtree
};
write functions which will traverse the tree in in-Order, Pre-Order and Post-Order.
solution:
In earlier questions related to tree, “Counting number of leaf nodes” and “Has-Path sum problem“, I have written that tree algorithms are better written using recursive algorithms. These traversal algorithms also are easy if we write them recursively.
For demo purpose consider the below tree.
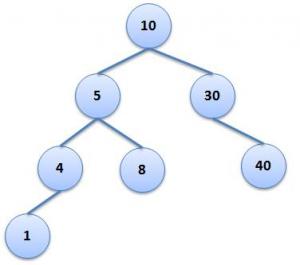
The three traversals (pre, in and post order) are named so because of the positioning of root node w.r.t the left and Right sub tree. In pre-order traversal, you visit the root node, then you visit the left subtree in pre-order traversal and then the right subtree in pre-order. In In-Order, we traverse the left subtree in In-Order then we visit the root and finally the Right sub-tree in In-Order, Similarly in Post-Order traversal.
Lets start our traversals:
Pre-order traversal
Visit the root node first (pre)
Algorithm:
1. Visit the root (we will print it when we visit to show the order of visiting) 2. Traverse the left subtree in pre-order 3. Traverse the right subtree in pre-order
Code:
/* Print Pre-order traversal of the tree */
void preOrder(node* r){
if(r){
cout << r->data << " ";
preOrder(r->left);
preOrder(r->right);
}
}
Output:
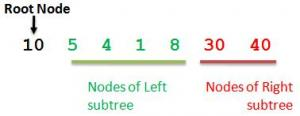
10 5 4 1 8 30 40
The root node comes before the left and right subtree (for every node of the tree)
In-order traversal
Visit the root node in between the left and right node (in)
Algorithm:
1. Traverse the left subtree in in-order 2. Visit the root (we will print it when we visit to show the order of visiting) 3. Traverse the right subtree in in-order
Code:
/* Print In-order traversal of the tree */
void inOrder(node* r){
if(r){
inOrder(r->left);
cout << r->data << " ";
inOrder(r->right);
}
}
Output:
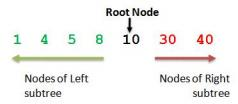
1 4 5 8 10 30 40
You may want to observe in the output that root lies in between the left and right traversals.
Post-order traversal
Visit the root node after (post) visiting the left and right subtree.
Algorithm:
1. Traverse the left subtree in in-order 2. Traverse the right subtree in in-order 3. Visit the root (we will print it when we visit to show the order of visiting)
Code:
/* Print Post-order traversal of the tree */
void postOrder(node* r){
if(r){
postOrder(r->left);
postOrder(r->right);
cout << r->data << " ";
}
}
Output:
1 4 8 5 40 30 10

1 Comment
[…] To learn more about traversals see our previous question on Basic Tree Traversals. […]