Binary Heap

Binary heap is used to implement Priority queue. It is an array object, visualized as an almost complete binary tree. Binary heap comes in two flavours

• Max-Heap
• Min-Heap

A max-heap is an almost complete binary tree, where, value at each node is greater than the value of its children. Similarly, a min-heap is an almost complete binary tree where value at a node is less than both its children (unless it is a leaf node and does not have any children).

Below picture gives an example of max and min heap, and how they are actually stored in an array:

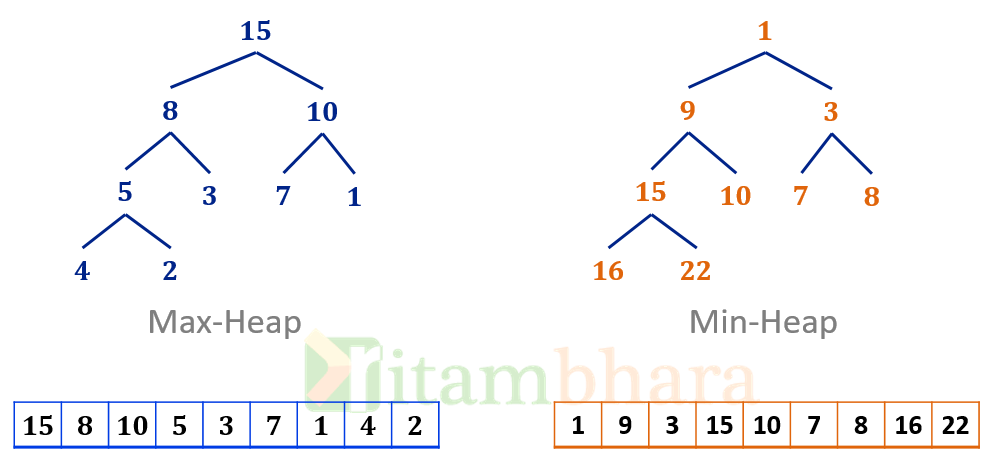
If you don’t understand the relation between tree and array, please read my previous article here…
[rapid_quiz question=”An array sorted in decreasing order is a Max-Heap” answer=”True” options=”True|False” notes=”Take any such array and try to represent it in the form of a tree, it will satisfy all properties of Max-heap.”]
[rapid_quiz question=”Which of the below arrays are heaps?” answer=”5 14 10 27 17 11″ options=”15 19 10 7 17 16|5 14 10 27 17 11″ notes=”Draw the corresponding tree.”]
[rapid_quiz question=”The largest element in a Max-Heap can be anywhere in the tree. ” answer=”False” options=”True|False” notes=”The largest element will always be at the root. Second largest will be at distance 1 from root and so on.”]
[rapid_quiz question=”How many leaf elements will be there in the heap of size n?” answer=”ceiling of (n/2)” options=”n/4|ceiling of (n/2)|floor of (n/2)|can’t be determined” notes=”Try with some values, if there are 3 nodes then 2 of them will be leaf. If there are 4 nodes then also there will be 2 leaf nodes. “]
[rapid_quiz question=”Which of the two statements about max-heap is/are correct? A) All paths from root to leaf are in nonincreasing order. b) Left and right sub-trees are unrelated” answer=”Both A and B” options=”Only A|Only B|Both A and B|None” notes=””]

Heapify operation

This is an important operation in the implementation of Binary heap.

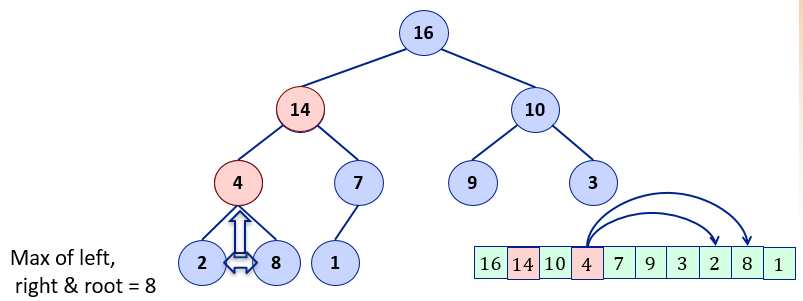
Given a max-heap (in the form of Array). A node r in the heap which violate the heap property, as shown below.

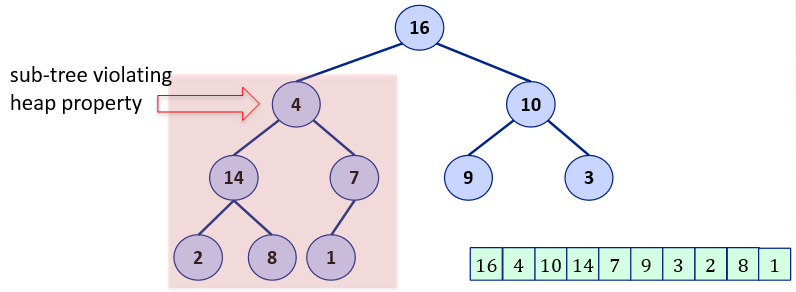
Note that all the children of Node ‘4‘ are following the heap property, Its only the root of this sub-tree where the violation is. If such is the case then heapify operation can fix it and restore the heap property of the subtree. The procedure of heapify is:

1. Compare the below 3 and find the maximum value:
    a. Value at root node
    b. Value of left child
    c. Value of Right child
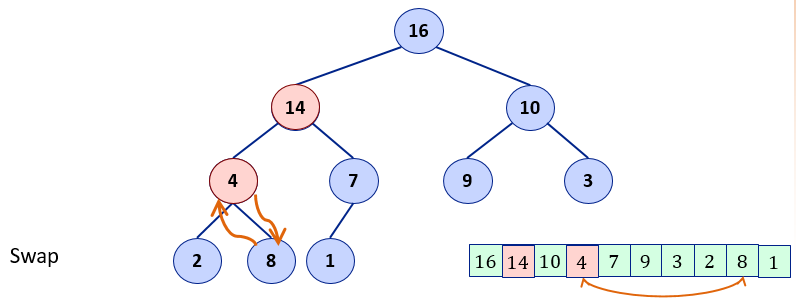
2.If value at root is not maximum then swap root with the maximum value.
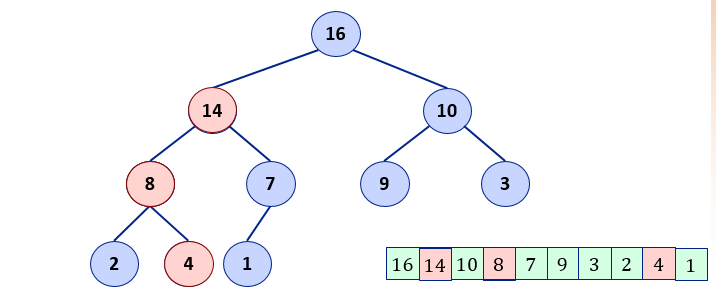
3. Run Heapify for the child whose value was swapped in step-2.

Let us see it in picture, Have a look at the actual changes that take place in the array (shown on the bottom right of each picture):

1. Find maximum of root (4) and its two children

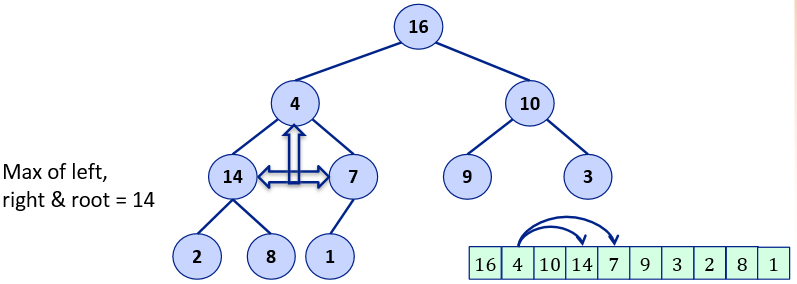
2. Swap root of subtree with max value

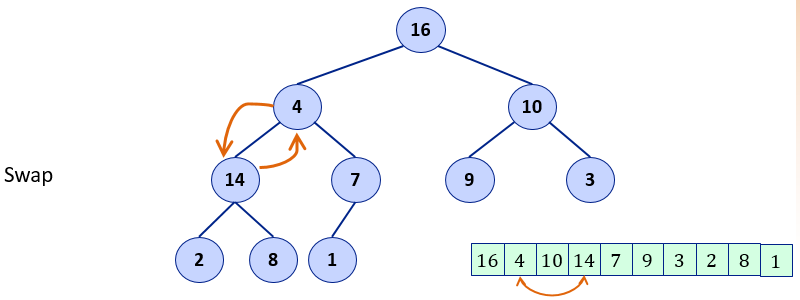
3. Repeat the same for subtree whose root was swapped

After the heapify operation the array is a valid max-heap

Below is the code of Heapify

void heapify(int *arr, int n, int root)
{
	(root <= n/2)		// Leaf nodes are already heapified
	{
		int max=root, lptr=2*root + 1, rptr=2*root + 2;
		if(lptrarr[max])
			max = lptr;	// LEFT Child is Max
		if(rptrarr[max])
			max = rptr;	// RIGHT Child is Max
		if(max != root)
		{
			swap(&arr[root], &arr[max]);
			heapify(arr, n, max);
		}
	}
}

Time taken by the above algorithm is O(lg(n)), because we are doing constant amount of work at each level and can be at most O(lg(n)) levels. In best case the the time taken can be O(1) when root is already maximum of there are no children of the node under consideration.

Extra memory will be taken since we are using recursion.

Build Heap Operation

This operation takes any random array as input and converts it into a heap.
The heap is built in a bottom-up manner. We start from the last element. Since the leaf nodes does not require any action, we skip all the leaf nodes and start from the first non-leaf node from the end and work backward.
As we saw above and in Almost complete Binary tree, that there in a heap of n integers half will be leaf nodes (actually ceiling of (n/2)).  So we start from index n/2 downto index zero and call the heapify operation for each node.
Code:

void buildHeap(int *arr, int n)
{
	int i=0;
	for(i=n/2; i>=0; i--)
		heapify(arr, n, i);
}