Linear Search in detail
June 29, 2013Optimized bubble sort algorithm
June 30, 2013Binary Search or Half-interval search
 Binary search is a Divide & Conquer algorithm used to search for an element in the array. It requires the array to be sorted. If array is not sorted then the only way to search in the array is Linear search.
Binary search is a Divide & Conquer algorithm used to search for an element in the array. It requires the array to be sorted. If array is not sorted then the only way to search in the array is Linear search.
Binary search divide the number of elements to be searched in two halves in each iteration and only one half remains relevant to be searched and the other is ignored. Therefore, even if the element is not present in the array we don’t need to traverse all the element in the list.
It keep three variables low, high and mid, each storing the index of first element, last element and middle element in the array being searched.
Initially value of low (L) will be 0 (position of first element of array), high(H) will be n-1 (position of last element in the array) and we are searching in the entire array, then the size reduces to half and we either search the first half or the second half depending on whether element at mid is greater than less then the element being searched.
Algorithm:
// position of first and last element
1. low = 0; high = n-1;
2. If low is greater than high // entire array is searched
RETURN -1 // NOT FOUND
3. mid = (low+high)/2
4. IF (element at mid == Searched value)
Element FOUND. Return the index.
ELSE
IF (element at mid < Searched value)
//Go to the step 2 for the part of the array, before mid.
high = mid-1;
GOTO step 2.
ELSE // element at mid > searched element
//Go to the step 2 for the part of the array, After mid.
low = mid+1;
GOTO step 2.
Below pictures shows the working of algorithm:
Let the array be {6, 13, 14, 25, 33, 43, 51, 53, 64, 72, 84, 93, 95, 96, 96}, and let the data to be searched is 33.
1. Since arr[L] <= data <=arr[H].
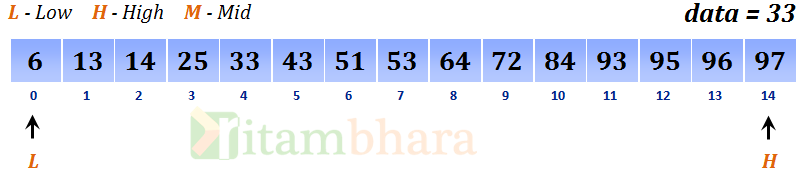
2. Calculate mid, M = (L+H)/2

3. Since data<arr[M], and all elements on the right of M will be greater than arr[M], hence we can ignore the elements on the right of M and never need to search in arr[M] – arr[H].

Note: This is not there in linear search. We can never ignore anything in linear search.
4. L and H area adjusted according to the new bounds and M is calculated again.

5. Since arr[M] < data. the value cannot be present on the left side of M (including M).

6. Calculating M again, and then checking it against data.

7. updating L and H again.

8. Calculating M = (L+H)/2.

9. arr[M] == data. Hence return M (index where data is found).

Code:
/** Non-Recursive Function */
int bSearch(int * arr, int n, int data)
{
int l=0, h=n-1, m;
while(l <= h)
{
m = (l + h) / 2;
if(arr[m] == data)
return m; // FOUND.
else if(arr[m] < data)
l = m + 1;
else
h = m – 1;
}
return -1; // NOT FOUND
}
Below is the recursive solution for Binary search
/** Recursive Function */
int bSearch(int * arr, int l , int h, int data)
{
if(l > h || arr[l] > data || arr[h] < data)
return -1; // NOT FOUND.
else
{
int m = (l+h)/2;
if(arr[m] == data)
return m; // FOUND.
else if (arr[m]<data)
return bSearch(arr, m+1, h, data)
else
return bSearch(arr, l, m-1, data);
}
}
Time Complexity:
Best Case: O( 1 ) Found at the middle of entire Array
Worst Case: O( lg (n) ) Not found
Average Case: O( lg (n) )
Space Complexity:
Non-Recursive: O(1)
Recursive: O( lg(n) )
Variations:
1. Write code to find the position of pivot in a sorted array rotated around a pivot.
Solution:
Step-1. Find position of pivot in the array using Binary Search. The condition for checking arr[mid] == data will be changed to see that it should be the last element in the first sub array.
if( (mid
2. A Sorted array is rotated around the pivot, write b-search algorithm to search in that array.
Solution:
Step-1. Find position of pivot in the array using Binary Search as shown in the first variation. Step-2: Once the position of pivot is found, perform binary search in the left sub array and right sub array independently.
3. Given an Array of numbers and a number x. Write function to search for two elements in the array, whose sum is x.
Solution: See this post.

1 Comment
I am collecting the best elements and required data from this post. I am getting some of storing information from online. My friend is sharing some of problems for fixing the elements. I am searching the best and wonderful function for making good data. it is really good for getting some of variables and different types of sizes. I have found the different types of application and analysis in online. I am developing more elements with designs available in that. This website is given the great post and articles about that. i need the best sources and experienced nature of points to solve the problem.
I am solving more problems with that website. More new points and desktop applications are given with this post. Thanks for this post. I am getting more developing points here. I need the great needs and required value here. I have supply more post like this. More users are taken their points and innovative matters. Now i am writing post for blog. It is getting all plans and tips for providing the great data in the pages. In this page is getting greater calculations and submitting good manner also. I am also adjusting the new idea with this. I am join with my friends for collecting more information like this.
My father is given structure and important design to make for the purpose of posting the pages. I need more information about the elements to posting that. I am getting stress for collecting the details from online websites. More websites are given great points about that. But I cannot know for it. I need your sources and way of solving the problem and list of steps are applied for that. You can given your points and reviews here. I am waiting for the best response