Check if all leaf nodes are at the same level

Given a binary tree write a function to check if all leaf nodes of the tree are at the same level. For example, In all the below trees, the leaf nodes are at same level:



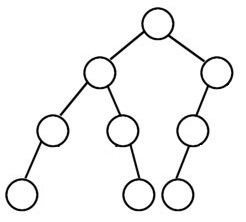
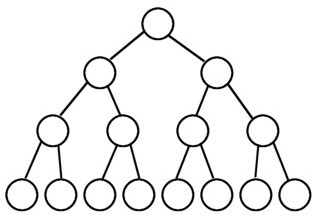
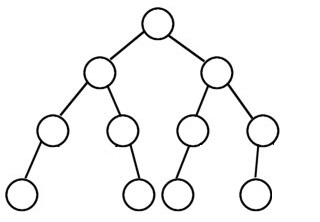
But in the below tree the leaf nodes are not at the same level:

   A           A              A
  / \         / \           /   \
 B   C       B   C         B     C
    /         \           / \
   D           D         D  E

Method-1: Calculate distance from the root:

This is similar to saying, that check if all leaf nodes are at the same distance from the root. This can be checked by making small changes in the BFS code to do level wise traversal.

Basically we have to check that, (the first leaf node is seen at the start of a level) AND (All the nodes after the first leaf node should also be leaf nodes)

Method-2:

Algorithm

This algorithm keeps track of the level of current node. It also has a static variable which will be set with the level of leaf node, when we encounter a leaf node for the first time. Every time we see a leaf node we check whether the level of this leaf node is same as the one set by us.. If no then this leaf node is at different level from the one found previously. Hence, return false, else continue till all the nodes are seen.

    1. Reset global variable, leafLevel = -1
    2. Traverse the entire tree. For each node:
    3. IF(current node is a leaf node)
          IF(leafLevel == -1)              // Not yet set
             leafLevel = level of Current Node
             RETURN true                   // Case when there is just 1 node
          ELSE
             IF(leafLevel == level of Current Node)
                 RETURN true;
             ELSE
                 RETURN false;
        ESLE
            call function recursively for left and right subtree and
                 return true if both of them returns true, else return false

Code:

/**
 * This function should not be called directly because it does not handle the case where r is null.
 * Either handle the case at the level of caller or call the next function (checkAllNodesSameLevel)
 */
int checkAllNodesSameLvlRecursive(struct node * r, int curLevel, int resetTopLevel)
{
    static int topLevel = -1;
    if(resetTopLevel)
        topLevel = -1;
    // If it is a leaf node, then take action.
    if(r->lptr == NULL && r->rptr == NULL)
    {
        // If it is the first leaf node encountered
        if(topLevel == -1)
        {
            topLevel = curLevel;
            return true;
        }
        else if(curLevel == topLevel)
            return true;
        else
            return false;
    }
    // Check the left and right subtree.
    int leftResult = true;
    int rightResult = true;
    if(r->lptr)
        leftResult = checkAllNodesSameLvlRecursive(r->lptr, curLevel+1, false);
    if(r->rptr)
        rightResult = checkAllNodesSameLvlRecursive(r->rptr, curLevel+1, false);
    if( !rightResult || !leftResult)
        return false;
    return true;
}
/**
 * Main function to be called from outside to check
 * if all leaf nodes are at the same level.
 */
int checkAllNodesSameLevel(struct node * r)
{
    if(r == NULL)
        return true;
    return checkAllNodesSameLvlRecursive(r, 0, true);
}

Time Complexity: O(n), Since we are visiting a node only once.