check if all nodes of a tree has only one child

Given the PreOrder traversal of a binary search tree (in the form of a tree), check if all the nodes (except the last) of the tree has exactly one child.

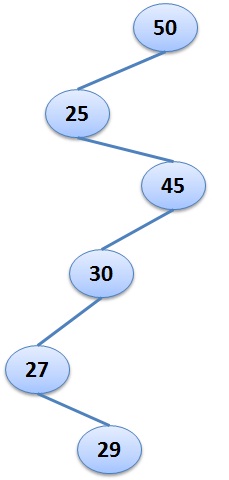
For Example: If the Preorder traversal of the tree is given as below:

{50, 25, 45, 30, 27, 29}

The the output should be: TRUE
Because Binary Search Tree represented by the above traversal is shown on the right.
In the tree, EACH NON-LEAF NODE HAS EXACTLY ONE CHILD.

Solution:

In preorder traversal, we first visit the Root Node then the left Sub-tree and then right sub-tree. So all the descendants of a Node appears on the right in the pre-order traversal.

If a particular Node has only one child, then all the descendants are either on the Right sub-tree or left sub-tree. Hence the descendants are either All greater than the Node, or ALL less than the Node.

Now there can be multiple methods to check this thing (if descendents are either all greater than this or all les than this) in the array:

1. Brute-Force (Using two loops) – O(n²) time 

bool checkTree(int *arr, int n)
{
    bool larger;
    for(int i=0; i<n-1; i++)
    {
        if(arr[i+1] > arr[i])
            larger = true;
        else
            larger = false;
        for(int j=i+1; j<n; j++)
            if( (larger && arr[j] < arr[i]) || (!larger && arr[j] > arr[i]) )
                return false;
    }
    return true;
}

2. Using max-min pointers – O(n) time

1. Make min & max point last element.
    min = max = n-1
2. for(i=n-2; i>=0; i--)
    arr[i] should be less than current min or greater than current max.

Code:

bool checkTree2(int *arr, int n)
{
    int min, max;
    min = max = n-1;
    for(int i=n-2; i>=0; i--)
        if(arr[i] < arr[min])
            min = i;
        else if(arr[i] > arr[max])
            max = i;
        else
            return false;
    return true;
}