Code to evaluate a postfix expression

Given an expression in postfix notation, write code to evalute a mathematical expression given in postfix notation. For Example:

Input: 4 2 3 + * 6 -
Output: 14

If you don’t know what is postfix notation or how can we convert a normal mathematical expression to postfix or prefix notation then read our previous article on this topic.
The expression 4 2 3 + * 6 – in in-fix notation (the way we usually write in mathematics) is 4 * (2 + 3) – 6, we talked about how to convert an expression from in-fix to postfix notation earlier. The value of this expression is 4*5-6 = 14.
Advantage of using postfix notation is that there is not brackets in this expression, hence the logic can be simplified because you don’t have to worry about handling the brackets.
If an expression is given in post-fix notation then we need a stack data structure to evaluate that expression (the way we used stack to convert an expression from in-fix to post-fix).

Algorithm:

The below algorithm is used to evaluate an expression given in post-fix notation:

Step-1: Read all the symbols(operators and operands) in the given post-fix Expression
        one by one from Left to Right and perform below steps on each of them.
    - If the symbol (that we have read in step-1) is operand,
      then push it in the Stack.
    - Else, if symbol is operator (+ , - , * , / etc.,),
      then pop TWO operands from stack and perform that operation
      (represented by symbol) on the two operands and push the result back in the stack.
Step-2: When all the symbols in the expressions are read then there
        will be just one value left in the stack.
        That is the final value of the expressions, just pop it out.

Let us see how the above algorithm applies on our expression. The expression given is

4 2 3 + * 6 -

You must have noticed, that we have kept all the numbers as single digit for simplicity sake.
Step-1: The first Symbol that we encounter in our expression while reading it from left to right is 4. Since 4 is an operand, we will push it in the stack.

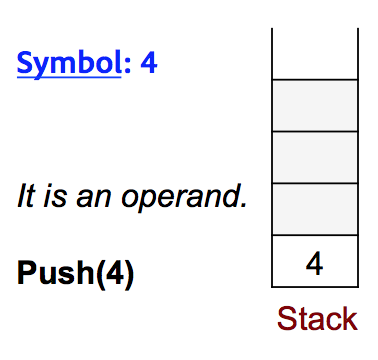
Step-2: Next symbol is 2, it is also an operand, and hence will be pushed in the stack.

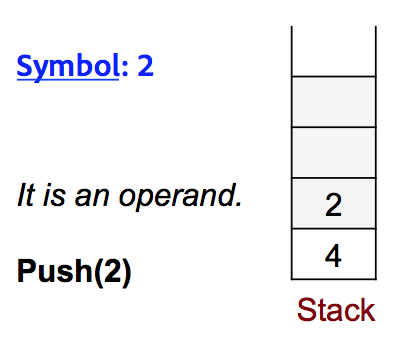
Step-3: Next symbol is 3, it is also an operand, and hence will be pushed in the stack.

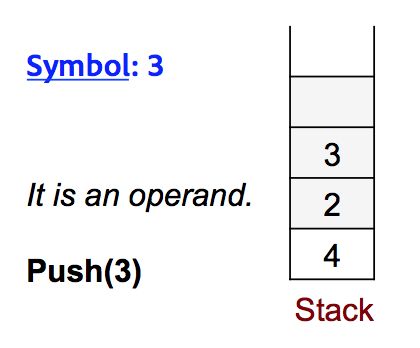
Step-4: Next symbol is the operator plus (+), When we encounter an operator, we pop the number of operands that this operator need (plus is a binary operator and needs 2 operands). So we pop out top two values, perform a plus operation on them and push the result back into the same stack.

Step-5: Next symbol is operator multiply, we perform the same steps as above.

Step-6: Next Symbol is an operator, 6, and it will be pushed into the array directly.

Step-7: Next symbol is operator minus, we pop two operands and perform the operation (notice the order of operands), and will push back the result of operation in the stack.

Step-8: Now the expression is complete, and hence there should be only one value in the stack which is the final value of the expression. If there are more than one values in the stack at this point, then either the expression is wrong, or you have made some mistake while evaluating the expression.
Hence result of expression is: 14.

Code:

/**
 * Checks if the given character is a numeric digit or not.
 * Returns true if it is a digit.
 */
bool isNumericDigit(char ch)
{
   return (ch>='0' && ch<='9');
}
int evaluatePostfix(char* expression)
{
   MyStack stack;
   // Read each symbol one at a time
   for (int i = 0; expression[i] != '\0'; ++i)
   {
      // If the scanned character is an operand, push it to the stack.
      if (isNumericDigit(expression[i]))
         stack.push(expression[i] - '0');
      //  If the scanned character is an operator, pop two
      // elements from stack apply the operator
      else
      {
         int a = stack.pop();
         int b = stack.pop();
         switch (expression[i])
         {
            case '+': stack.push(b + a); break;
            case '-': stack.push(b - a); break;
            case '*': stack.push(b * a); break;
            case '/': stack.push(b/a);   break;
         }
      }
   }
   return stack.pop();
}