Convert a Binary Tree to Binary Search Tree

Given a Binary Tree, write code to convert it to Binary Search Tree such that the structure of the tree remains the same. For example: Both the below trees

          5                        10
        /   \                    /    \
       8    10                  5     30
     /  \     \               /   \     \
    4   30     1             8    40     1
   /                        /
  40                       4

Should generate the below Binary Search Tree.

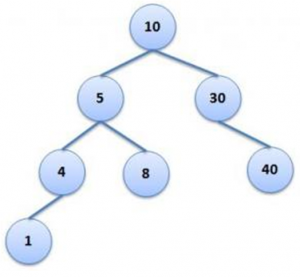
Note that the structure of the tree remains the same. Hence all the three trees above are Similar.

Solution:

For this we need an extra array of size n (Number of Nodes) to store the inorder traversal of the tree.

Algorithm:

1. Traverse the tree in inorder and store the values in array.
2. Sort the Array.
3. Traverse the tree again in in-order and copy the values from array in the Nodes.

Code:

/**
 * Populate the array arr with the inorder traversal of the tree pointed to by r.
 * pos holds a reference to the current poisition of arr.
 */
void populateInorderArray(Node*  r, int* arr, int* pos)
{
    if(r == NULL)
        return;
    populateInorderArray(r->lptr, arr, pos);
    arr[*pos] = r->data;
    (*pos)++;
    populateInorderArray(r->rptr, arr, pos);
}
/**
 * Traverse the Tree in Inorder traversal and copy the values from
 * array arr to the nodes of the tree.
 *
 * pos holds a reference to the current poisition of arr.
 */
void copyInorderArrayToTree(Node* r, int* arr, int* pos)
{
    if(r == NULL)
        return;
    copyInorderArrayToTree(r->lptr, arr, pos);
    r->data = arr[*pos];
    (*pos)++;
    copyInorderArrayToTree(r->rptr, arr, pos);
}
/** Functions accepts a pointer to the root of a Binary Tree
 * and converts it to Binary Search Tree.
 * We don't need a Node**, because we are not changing the root node,
 * We are only changing the value contained in the root node.
 *
 * Structure of the tree remains the same.
 */
void converttoBST(Node* r)
{
    if(NULL == r)
        return;
    // hard-codding it to 1000 for simplicity.
    // define the array equal to number of nodes.
    int arr[1000] = {0};
    int n = 0;    // Will hold the number of Nodes
    populateInorderArray(r, arr, &n);
    quickSort(arr, 0, n-1);
    n=0;
    copyInorderArrayToTree(r, arr, &n);
}

I am sure you can write the Quick Sort algorithm. Ok, let me write the function to sort the array also (as used in the above code).

/** Helper function to partition the array for a pivot.
 */
int partition(int *arr, int low, int high)
{
    int p = low;
    low++;
    while(low<=high)
    {
        while(arr[low]<arr[p]) low++;
        while(arr[high]>arr[p]) high--;
        if(low<high)
        {
            int temp = arr[low];
            arr[low] = arr[high];
            arr[high] = temp;
        }
    }
    int temp = arr[p];
    arr[p] = arr[high];
    arr[high] = temp;
    return high;
}
/** Function to sort the array using Quick sort algorithm
 */
void quickSort(int* arr, int a, int b)
{
    if(a>=b)
        return;
    int pos = partition(arr, a, b);
    quickSort(arr, a, pos-1);
    quickSort(arr, pos+1, b);
}

Time Complexity:

Time to populate Inorder Array = O(n)
Time to Sort Inorder Array = O(n.lg(n))
Time to Put values from Sorter array to Tree = O(n)
Total Time = O(n) + O(n.lg(n)) + O(n) = O(n.lg(n))

Note: The above implementation of Quick sort takes O(n²) time in worst case, because we are not choosing the pivot randomly. But a randomized Quick Sort algorithm takes O(n.lg(n)) time in the worst case.
Extra Space Used: O(n)
Note: The array uses extra space O(n). even if we do not use the array, the Inorder algorithm takes O(n) space because of Recursion.