Generic pointers in C language
May 13, 2017Count frequency of a number in a sorted array
May 26, 2017Counting Sort
It is used when there are few unique elements in an array. Counting sort takes O(n+k) time in the worst case, where n is number of elements and all the elements are in the range 1 to k (both inclusive).
In this algorithm, we count the occurrences of each number and then put the numbers in their required position in the output array.
Let us first illustrate how counting sort works and then we will see its code and analyze its running time. For simplicity let us assume that all the numbers given are in the range 0 to 5, the input array is
int arr[] = {1, 2, 1, 3, 1, 5, 2, 0, 2, 5}
We take a count array to store the number of occurrences of each number. Since total numbers possible are six, we take the count array of size 6
int count[6] = {0};
Now, compute and store the count of each unique element in the array, such that count[x] stores, the total number of times x appears in array arr. The code for this is straight forward.
for(int i=0; i<n; i++)
count[arr[i]]++;
After this for loop is executed, the count array will become:
![]()
Next step is to modify each element in the count array, so that each index stores sum of count of occurrences of all the numbers less than or equal to current index. The logic is to just add all previous values to current index.
for(int i=1; i<=k; i++)
count[i] += count[i-1];
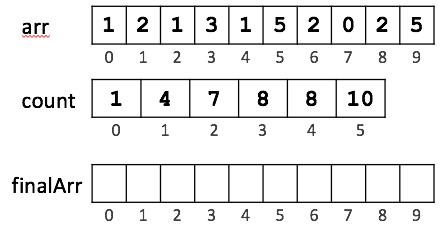
After this for loop, count array becomes
![]()
count[x] now contains the position at which the last occurrence of x will appear in the sorted array. For example, the last occurrence of 5 will be stored at position 10 (index 9).
We keep an auxiliary array, say finalArr, of the same size as arr to hold the final sorted result.
Now we traverse the array arr backward, the first element found is 5 (at arr[9]), from count array, we know that 5 need to go to position 10 (index-9) in the final array. Store 5 to position finalArr[count[5]-1]. Now if the next occurrence of same value, 5, is seen in the array arr later it should be placed at position 9 (just before this occurrence).
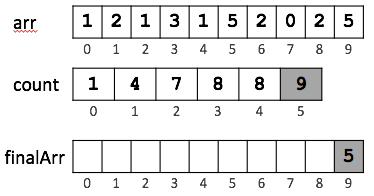
What we are doing is:
for(int i=n-1; i>=0; i--)
{
finalArr[count[arr[i]]-1] = arr[i];
count[arr[i]]--;
}
Below code shows the complete code for counting sort.
void countingSort(int *arr, int n, int k)
{
int count[k+1]; int finalArr[n]; int i;
// INITIALIZING COUNT ARRAY WITH 0's
for(i=0; i<=k; i++)
count[i] = 0;
// COUNTING NUM OF OCCURRENCES OF EACH NUMBER
for(i=0; i<n; i++)
count[arr[i]]++;
for(i=1; i<=k; i++)
count[i] += count[i-1];
for(i=n-1; i>=0; i--)
{
finalArr[count[arr[i]]-1] = arr[i];
count[arr[i]]--;
}
// STORING THE ARRAY BACK TO ORIGINAL ARRAY.
for(i=0; i<n; i++)
arr[i] = finalArr[i];
}
Analysis of counting sort
Counting sort takes O(n+k) time and O(n+k) extra memory. If numbers are in the range 0 to n2, then time taken by counting sort will be O(n2), which is worse than the O(n.lg(n)) comparison sorting algorithm, but, if the range is small, counting sort can sort the array in linear time taking linear extra memory.
We may choose to use a hash instead of the count array, this will reduce the extra memory taken in the worst case to O(n), even if the numbers are in the range 0 to n2.
It is not comparison based sorting, since we are not comparing elements with each other. It can be verified that the sorting is stable, if there are two occurrences of an element in the input array, then after sorting, the relative order of these two elements remain unchanged.
Counting sort is used as a sub-routing in other sorting algorithms.
