Find non repeating number

Given an array of numbers where each number is repeating thrice. In that array one element is not repeating at all. Find that number.

Input Array: {5, 9, 2, 5, 2, 5, 2}
Output: 9

Brute-Force method:

For each element check if it is repeating or not. If it is not repeating then return it.

Time complexity: O(n²)
Extra Space: O(1)

Using Sorting:

Sort the array. Now repeating elements will be adjescent. Hence the check of ‘whether a number is repeating or not’ can be made in O(1) time. But Sorting will take O(n.lg(n)) time 

Time complexity: O(n.lg(n))
Extra Space: O(1)

 1. QuickSort(arr)
 2. for(int i=0; i<n; i+=3)
       if(i == n-1 || arr[i] != arr[i+1])
           return arr[i];

We are incrementing i by

i += 3

because it is given that each element (except for 1) is repeating thrice (not 3).

Also note the check

if(i == n-1 || arr[i] != arr[i+1])

we need (i == n-1) for case when the single element is the largest. In this case the single element will come at the end of array, hence arr[i+1] will cross the upper bound.

Using Hashing:

 We can keep the count of number of times an element is repeating in a hash.

At the end we will just check the hash and see for which element the repeatCount is 1. That number will be the answer. The drawback back in this case is that extra space is required.

Time complexity: O(n)
Extra Space: O(n)

Best Solution O(n)-time and O(1)-Space:

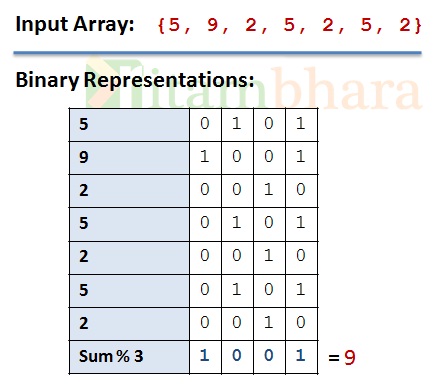
1. Sum the bits of all the numbers at each position.
2. Take the modulo with 3 of the sum (for each bit-position)
3. Keep 1 for the bit-positions where modulo with 3 is non-zero.
   Those are the bit-positions of the result.

Time complexity: O(n)
Extra Space: O(1)

Example: If the input array is {5, 9, 2, 5, 2, 5, 2} then,

Code:

#define BITS_IN_AN_INTEGER 32
/**
 * Return the non-repeating element in the array where all the elements
 * are repeating three times except for one which is not repeating at all.
 */
int getNonRepeating(int* arr, int n)
{
    int nonRepValue = 0;
    // For each bit in an integer.
    for (int i = 0; i < BITS_IN_AN_INTEGER; i++)
    {
      int sum = 0;
      unsigned int mask = (1 << i);
      // Sum of set bits at i'th position of all elements
      for (int j=0; j< n; j++ )
          if (arr[j] & mask)
            sum++;
      if (sum % 3)
        nonRepValue |= mask;
    }
    return nonRepValue;
}