Increment a number given in the form of linked list
March 10, 2015welcome to marriagefiesta
March 18, 2015Find popular element in an array
Given a sorted array of integers, find a “popular” element i.e. one which occurs more than n/4 times. If no such element exist (which occurs more than n/4 times) then print error.
For example: If Input array has 8 elements as below
{1, 3, 3, 3, 4, 6, 9, 10}
Then 3 is the popular element that comes three times.
Solution: Brute Force – O(n)
The brute force method will traverse the array linearly and for each element ‘i’ it will check
if(arr[i] == arr[i+n/4]) // arr[i] is popular elment else // Continue with other element
It will take O(n) time to find the popular element using above algorithm. Since the array is sorted, we can take advantage of some binary search type logic to reduce the time taken to lg(n).
lg(n) time algorithm
This is a two part algorithm, first we find the candidate and then we check whether any of the candidate is a popular element.
If we divide the array in 4 parts, then popular element will be first element of one of the four parts.
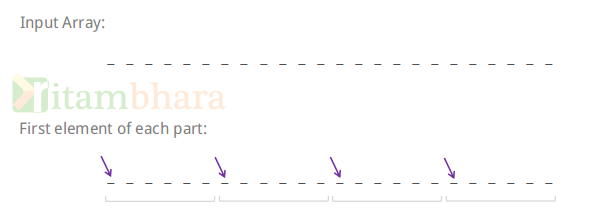
So, no matter how big the array is, there will always be 4 candidates for popular elements. Now, given these 4 candidates, we need to check if any one of them is popular element. To check this, for each of the 4 candidates:
- Find first occurrence of this number in the array (it may not be at i-n/4). This takes O(lg(n)) time.
- If first occurrence of the element is at index k, then check if the same element is also at arr[k+n/4]. This takes constant time
The time taken by this approach is sum of below three number
- Time taken to find 4 candidates – O(1)
- 4 * time taken to find first occurrence of each candidate – O(lg(n))
- 4 * Check each element whether or not it is popular – O(1)
The main logic in the solution is to find the first occurrence of a particular element in a sorted array using modified binary search.
/* Given Sorted array of size n, this function will return first occurance
* of element 'd' in array.
*/
int bSearch(int* arr, int n, int d)
{
int l = 0; int h = n-1;
while(l<h)
{
int m = (l+h)/2;
// First 2 cases are normal case.
// 3rd & 4th case means that (arr[m] == d)
// 3rd case is when we have reached the 1st occurrence of d
// 4th case is when arr[i] is not the first occurrence,
// In this case we will have to check the left side of m.
if(arr[m] < d)
l = m+1;
else if(arr[m] > d)
h = m-1;
else if(m == 0 || arr[m-1] < d)
return m;
else
h = m-1;
}
return -1;
}

3 Comments
it doesnt work for number at the lowest index
Could you please complete code for the binary search method. I want to see how input is partitioned and fed to binary search
public void findElementsThatApprearNbyKTimesUsingSorting(int[] input, int k) {
if (input == null || input.length == 0)
return;
Arrays.sort(input);
int i = 0, start = 0, end = -1, n = input.length;
while (i++ < k) {
start = end + 1;
end = start + n / k – 1;
int index = findFirstOccuranceOfANumberInSortedArrayUsingBinarySearch(input, start, end, input[end]), temp = index + n / k – 1;
if (index != -1 && temp < n && input[temp] == input[end])
System.out.print(input[index] + " ");
}
System.out.println();
}
private int findFirstOccuranceOfANumberInSortedArrayUsingBinarySearch(int[] input, int start, int end, int num) {
while (start <= end) {
int mid = (start + end) / 2;
if ((mid == 0 || input[mid – 1] = num)
end = mid – 1;
else
start = mid + 1;
}
return -1;
}