Hamming distance

Write code to calculate hamming distance between two strings.

Hamming distance between two strings of equal length is equal to the total number of positions at which corresponding characters in the two strings are different.

   String-1       String-2     Hamming distance
 ------------   ------------   ----------------
  TONED           ROSES               3
  KAMAL           RAWAT               3
  203             233                 1
  RITAM           BHARA               5
  OK              TATA                infinite (not equal sized)

If size of two strings is not same then the hamming distance between them is infinite.

Hamming Distance is more used in state algorithms. For example, in the below picture

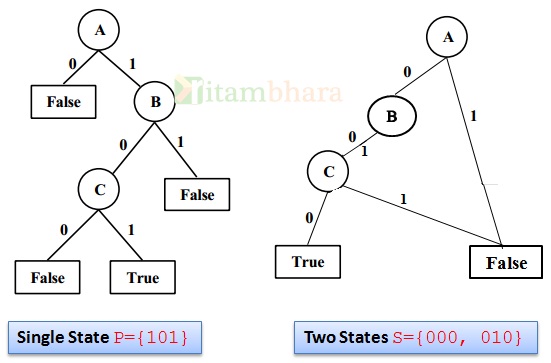
State P is a single state {101}, and Set S has {000} and {010}. (State is when we reach True starting from the top. If we reach False, then its not a valid state).
The hamming distance between {101} and {010} is three but the hamming distance between {101} and {000} is 2.
Another usefulness of hamming distance is when we want to calculate the different number of bits between two integers. For example, hamming distance between 6 (110) and 5 (101) is 2. But hamming distance between 6 (110) and 4 (100) is 1.

The Hamming distance can be interpreted as the number of bits which need to be changed (corrupted) to turn one string into the other. Sometimes the number of characters is used instead of the number of bits.

Hamming distance between two strings.

This is a simple algorithm. just traverse the two strings and seen how many characters mismatch.

Code:

/**
 * returns the hamming distance between string str1 and str2.
 * If hamming distance is infinite, then returns -1.
 */
int hammingDistance(char* str1, char* str2)
{
    // If any of the string is null
    // or they are not of the same size, then Hamming distance cannot be calculated.
    if(str1 == NULL || str2 == NULL || strlen(str1) != strlen(str2))
        return -1;
    int len = strlen(str1);
    int hDistance = 0;
    for(int i=0; i<len; i++)
        if(str1[i] != str2[i])
            hDistance++;
    return hDistance;
}

The above code is case sensitive (‘A’ and ‘a’ will be treated different). If you want it to be case insensitive, then make the corresponding changes in the comparison.

Time complexity: O(n).
Extra Space used: O(1).

Hamming distance between two integers

With integers there the problems that the strings are not equal will never come because number of bits will always be same. The algorithm is very simple. It uses two facts of bit-twiddling

1. XOR of two numbers will have the corresponding bits set which are different in the two numbers. (If two bits are same there XOR will be zero, if they are different their XOR will be 1).

Hence, 101 XOR 110 = 011 (2’nd and third bits are different, and they are set in the XOR)

2. You can turn off the rightmost set bit in a number, n, by taking its bitwise AND with (n-1). read this post for more detail.

Problem of finding number of different bits = calculate number of set bits in XOR.

Code:

/** Calculate hamming distance between x and y.
 * i.e the number of bits which are different between x and y
 */
unsigned int hammingDistanceInt(unsigned int x, unsigned int y)
{
    unsigned int hDistance = 0;
    // XOR will be 1 for bits that are different in x and y
    unsigned int diffBits = x ^ y;
    while(diffBits)
    {
        hDistance++;
        diffBits = diffBits & (diffBits - 1);
    }
    return hDistance;
}

Note: Time Complexity of above algorithm is O(n) where n is not the total number of bits, but number of bits that are different (Hamming distance). Hence if two numbers are same (hamming distance=0), then this algorithm will take constant, O(1) time.