Hashing introduction

Let us design a data structure in which we want to store numbers (taking it for simplicity, else it can be anything). We want to minimise the time taken by the following three operations:

• Insertion, time taken to insert a new value.
• Deletion, time taken to remove an existing value.
• Searching, time taken to search for a value in the data structure and see if it is present or not.

Which data structure do you suggest ?

Let us consider following data structures to store numbers.

1. Array
2. Sorted Array
3. Linked List
4. Balanced binary search tree
5. Direct Access Table.

Arrays (non-sorted) will take O(n) time to search and delete. The insertion can be done in constant time (assuming enough space in the array exist, we can just insert the new value at the end).
For sorted array, binary search can be used to search in O(lg(n)) time, but insertion will become O(n) time operation.
Linked list is also like unsorted array, we may choose to always insert at head, hence taking O(1) time to insert. But deletion and searching takes O(n) time. Deletion takes O(n) time because it requires us first search the values to be deleted.
Balanced binary search tree is an optimisation over the linear time taken by above data structures. All the three operations takes O(lg(n)) time in this case.
A better solution is to use a direct access table (compare it with RAM) where each element can be accessed in constant time. For this to be possible we need to establish a link between the value and its address (we need some way to determine address from the given value). This function, that accepts a value and return address where this value is (or need to be) stored is called Hash function.
For given problem, let us say this hash function is:

// RETURN THE ADDRESS (inside hash array) OF GIVEN VALUE
int hash(int value)
{
  return value;
}

If direct access table is an array, then address is the index at which this value need to be stored. For simplicity let us assume that the address is same as value.
For below numbers

12, 3, 6, 9, 1, 5, 7, 2, 10

The numbers will be stored as below:

If numbers are repeating, then we may not be able to store information like this. An obvious optimisation is to store count of occurrences of number i at arr[i].

This way if a number is repeating then its count will be incremented by one. This is used in many problems, look at the problem of printing characters occurring maximum number of times in a string.
This is the most basic hash.
There are many problems with this solution. First problem is that, we are wasting lot of space. arr[0], arr[4], etc. positions are all empty. If maximum value is 1000 and there are just 10 unique numbers, then 990 positions will be practically empty. This (direct access table) approach is hardly used as an alternate to hashing.
Hashing is the solution that can be used in almost all such situations and performs extremely well compared to above data structures like Array, Linked List, Balanced BST in practice. With hashing we get O(1) search time on average (under reasonable assumptions) and O(n) in worst case. 
The idea is to use Hash Function, that maps a big number or string or object to a small integer that can be used as index in hash table. A good hash function
1) is constant time and efficiently computable.
2)uniformly distribute the keys (Each table position equally likely for each key)
For example, if we are storing phone numbers, then a bad hash function is to take first two digits (because most of the times they will be same). A better function than this one is to consider last two digits. Please note that this may not be the best hash function. There may be better ways.
Hash table is an array that stores pointers to records corresponding to a given hash value (phone number). An entry in hash table is NIL if no existing phone number has hash function value equal to index for that entry.
If two numbers have same last two digits, then both of them end up having same hash values, and hence same index. This is called Collision.  Collision can be minimised, but it cannot be eliminated. There are many ways to handle collision.
For simplicity, let us store numbers in the table base on their last digit

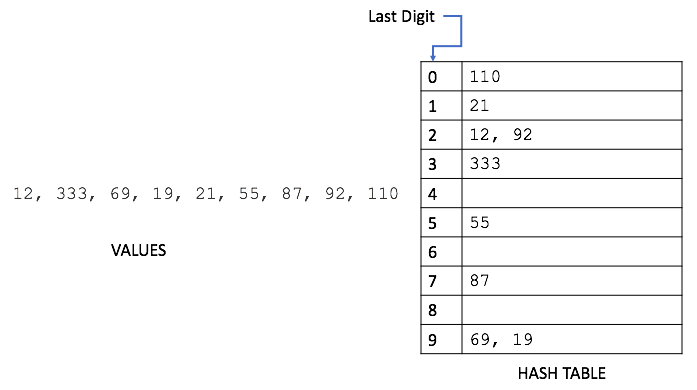
Last digit of 12 and 92 are same. Hash function return the same index (2) for both of these values. Hence, both of them need to be stored at index 2. This is collision. Following are the ways to handle collisions:

• Chaining:The idea is to make each cell of hash table point to a linked list of records that have same hash function value. Chaining is simple, but requires additional memory outside the table. In above figure, 12 and 92 will be two nodes of the linked list.
• Open Addressing: In open addressing, all elements are stored in the hash table itself. Each table entry contains either a record or NIL. When searching for an element, we one by one examine table slots until the desired element is found or it is clear that the element is not in the table.