Computing average of stream of numbers
June 11, 2012dynamic_cast in C++
June 11, 2012infix, prefix & postfix notations (Polish Notations)
What are Infix, Prefix and Postfix notations ?
Solution:
Infix, Prefix & Postfix notations are 3 different (but equivalent) ways to write a mathematical expression.
The ‘In’, ‘Pre’ and ‘Post’ in the notations represents the relative position at which operator will come:

Infix Notation:
Usual notation in constructing algebraic expression such that operator appears between two operands. It is ambiguous and requires knowledge of operator hierarchy for its evaluation. For example: If the expression is
A + B * C
Then we should know that we have to perform the multiplication (B*C) before the addition. Hence, the expression is evaluated as A+(B*C) and is different from (A+B)*C.
Parentheses can also be used to override operator hierarchy. So if an expression is
(A + B) * C
Then the addition will be performed before the multiplication.
The usual rules of ‘Order of Evaluation’ and Associativity also comes into picture in this form of notation.
Prefix Notation:
Operators are written before the operand. This is also called Polish Notation.
Hence, A+B will be written as +AB. The expression A+B*C is an Infix expression and the equivalent Prefix expression will be +A*BC. the conversion from Infix to Prefix will be done as below:
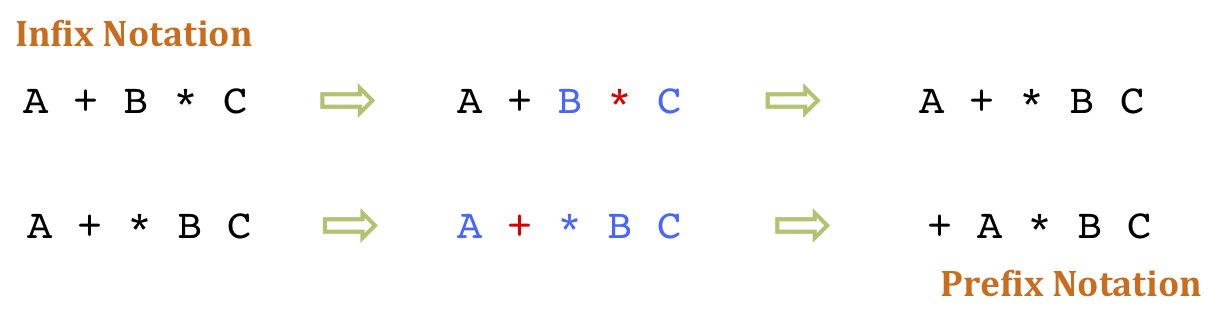
The operator in Red color is the operator under consideration (while converting from Infox to Prefix) and operands in blue are the operands under consideration (Note that *BC is the single operand of + operator).
Postfix Notation:
Operator comes after the Operand. This is also called ‘Reverse Polish’ Notation.
Hence, A+B will be written as AB+. The expression A+B*C is an Infix expression and the equivalent Postfix expression will be ABC*+. The conversion (from Infix to Postfix) will be as below:
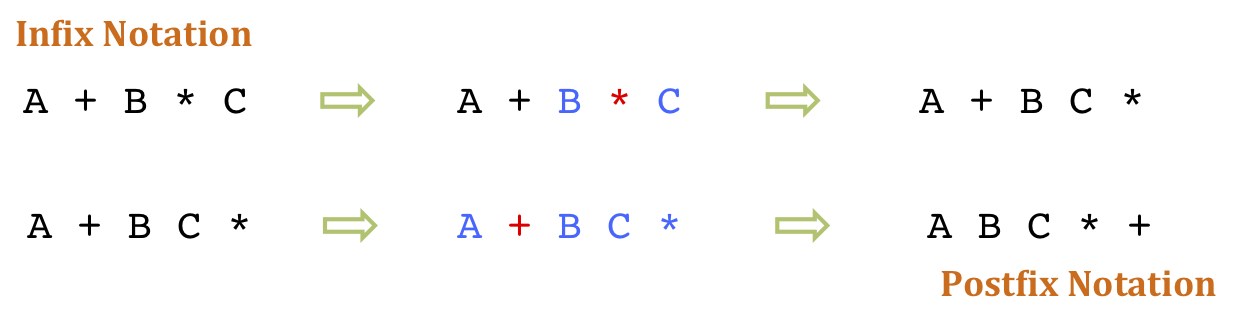

1 Comment
Awesome! Thanks your sharing!