Insertion Sort

Insertion sort is the most common sorting technique used by card players to sort their cards. It sorts the array in-place and is the one of the best comparison sort algorithms.
The list is divided into two parts the way we did in Selection sort. Pick the first element from the unsorted list and insert it at the right position in the sorted list (so that the sorted list is still sorted) as shown in the below example:
Example: Let the given array is as shown below, initially all the elements are in the unsorted part of the array.

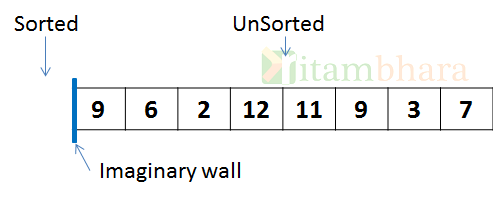
Since, single element is always sorted, we will move first element in the sorted list, and start with the second element (i=1)

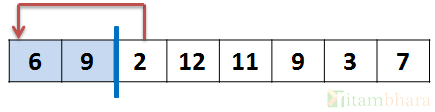
i=1, element at i (6) will be moved to its position in the sorted array.

i=2, element 2 will be moved to its proper position by shifting 9 and 6 toward right and inserting 2.

i=3, element 12 inserted at it proper position in sorted array.

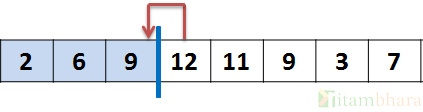
Similarly other elements are inserted at their right positions in the array and finally the entire array will be sorted.
Code:

/** Non-recursive Insertion Sort */
void insertionSort(int *a, int n)
{
    // For each element in the array
    for(int i=1; i<n; i++)
    {
        int j, temp = a[i];
        // Shift the element to right till we get an element smaller than
        // current element or end of list.
        for(j=i-1; j>=0 && a[j] > temp; j--)
            a[j+1] = a[j];
        // inserting element.
        a[j+1] = temp;
    }
}

Time Complexity:

Best Case: O(n) – When the array is already sorted in ascending order (In that case there will be only 1 check per element, hence O(n))
Worst case: O(n²) – When the array is sorted in reverse(descending) order. In that case each element will be inserted at the beginning of the list. Hence for k^th element there will be (k-1) comparisons. So total work required = 1 + 2 + 3 + … + n-1 = n(n-1)/2 = O(n²)
Average Case: Though theoretically the complexity is O(n²), practically it is less.

 The constant factor of Insertion Sort is very tight (less), in comparison to other sorting algorithms. This makes it an obvious choice, if number of elements is small.
If the array is almost sorted, then also Insertion sort is a very good choice. This is because for such cases (almost sorted arrays) insertion sort takes O(n) time and gives the best case performance.