Making tree from traversals

Given the pre-order and in-order traversal of a Binary Tree. Construct the tree from these traversals.

InOrder: 1 4 5 8 10 30 40
PreOrder: 10 5 4 1 8 30 40

Can you construct the Tree if only post-order and in-order traversals are given?
Can you construct a tree if only pre-order and post-order traversal of the tree is given?

Solution:

To learn more about traversals see our previous question on Basic Tree Traversals.

Given traversals are :

InOrder: 1 4 5 8 10 30 40
PreOrder: 10 5 4 1 8 30 40

In a PreOrder traversal the first element (leftmost) is the root of the tree. Hence, 10 is the root of our Binary Tree.

If we search 10 in InOrder traversal, we can say All elements on the left side of 10 in InOrder traversal are in the left sub-tree of 10 and all elements on the Right side of 10 are in the Right subtree of 10. Hence, in the first step, we are able to find out, that our tree will look something like this

       10
      /  \
     /    \
    /      \
1 4 5 8   30 40

If we recursively follow the above steps for left and Right subtrees also, we can find the entire tree.

For example:

• In the Right-subtree, we have 30 & 40, Now in Preorder, 30 comes first, so 30 is at the root ( in preorder, root comes first).
• Now 40 can be the right-child or left child of 30 (this is not clear from pre-order, for this we will have to look into in-order)
• In in-order traversal, 40 comes after 30 , hence 40 is right child of 30 (in in-order, root comes in between left and right child)

Hence, the Right sub-tree of 10 is constructed as below:

       10
       /  \
      /    30
     /      \
 1 4 5 8    40

Similarly, we can construct the left subtree of 10.

The final tree will be as shown below:

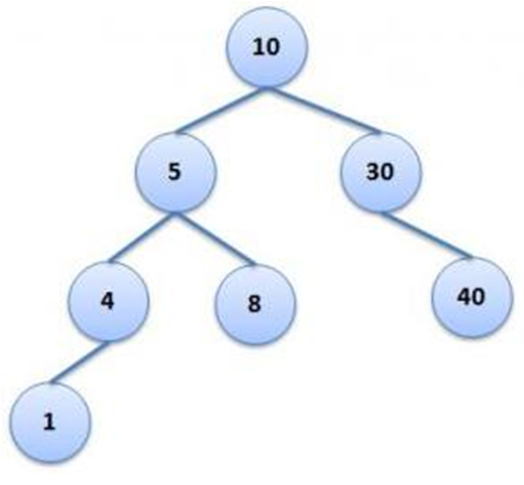
Can you construct the Tree if only post-order and in-order traversals are given?

Yes.

The logic will remain similar to the above (when in-order & pre-order is given). Except, in post-order traversal the last element (rightmost) will represent the root of the tree.

Can you construct a tree if only pre-order and post-order traversal of the tree is given?

No.

From both the orders (pre & post) we will be able to find the root of the binary tree, but we will not be able to separate elements on the left & right side of the tree, from any one of them.