Reversing a doubly linked list
July 1, 2015Upstream-Downstream relative speed question
September 24, 2015Minimum number of platform required for a railway station
Given arrival and departure times of all trains for a particular railway station, write code to find the minimum number of platforms required on that railway station, so that all trains can run according to their schedule.
Input can be in any form, but we essentially need two information about each train, the arrival time and departure time. Since we need to return only the minimum number of platforms and not the schedule of the trains, we don’t need other informations, like, name of the train, etc.
So, if the input is as given below:
Arrival Time Departure Time Train-1 9:00 9:15 Train-2 9:35 11:45 Train-3 9:45 11:05 Train-4 11:00 12:00 Train-5 14:30 18:15 Train-6 18:00 19:00
then we need at least 3 platforms, otherwise the railway station will not be able to accommodate all the trains.
First let us receive the input in the form of two arrays, first array holding all the arrival times, and second array holding all the departure time. For the above input, the two arrays will be:
double arivl[] = {9.00, 9.58, 9.75, 11.00, 14.00, 18.00};
double deprt[] = {9.25, 11.75, 11.08, 12.00, 18.25, 19.00};
Minimum number of platforms needed on the railway station is equal to the Maximum number of trains that can be there at any given time on the railway station.
Solution:
One way to get this number is to find the number of intervals (arrival till departure is one time interval) that every train time is overlapping with. The maximum out of all these numbers is the number of platforms needed.
int maxOverlaps = 0;
FOR i = 0 TO n-1
int numberOfOverLaps = 0;
FOR j = i+1 TO n-1
IF train[i] OVERLAPS WITH train[j] THEN
numberOfOverLaps++;
IF numberOfOverLaps > maxOverlaps THEN
maxOverlaps = numberOfOverLaps;
RETURN maxOverlaps;
But the above algorithm takes O(n2) time. We can optimize this by using the below greedy programming solution.
Solution -2: O(nlg(n)) time
Let’s draw all the trains arrival and departure on the railway station on a timeline:
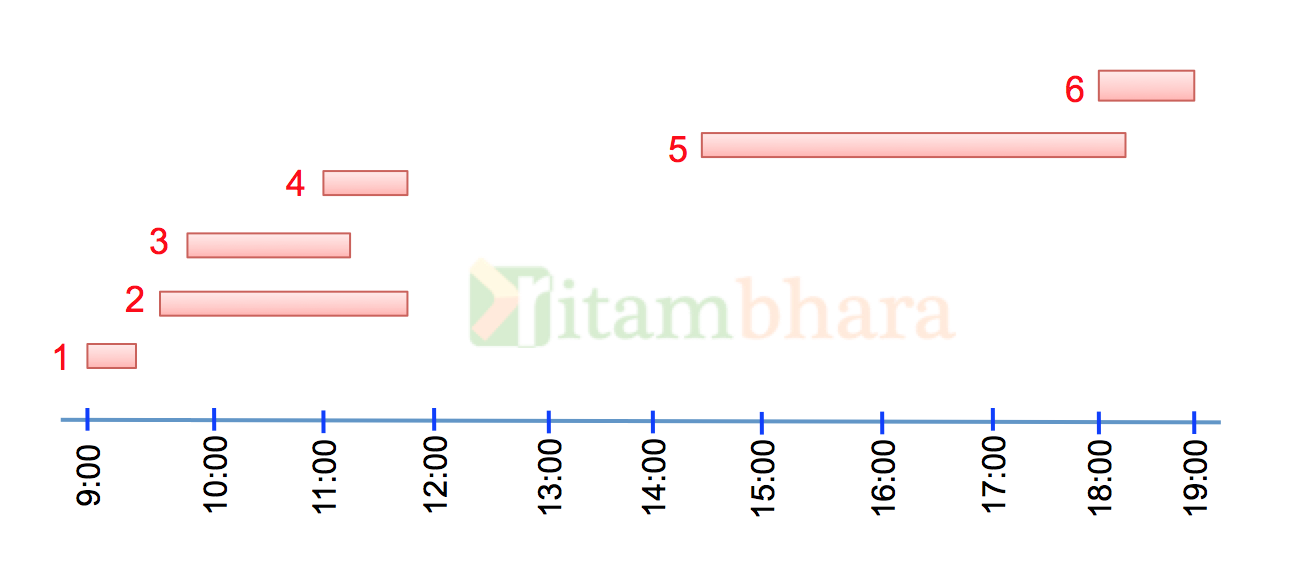
At any point (or arrival or departure) we calculate the total number of trains on the platform. Between time 11:00 to 11:05 there are 3 trains on the station, and this is the maximum number of trains present at any given time on station. Hence the minimum number of platforms required is 3.
We gave the above answer using intuitive logic. Now, let us write a program for the same:
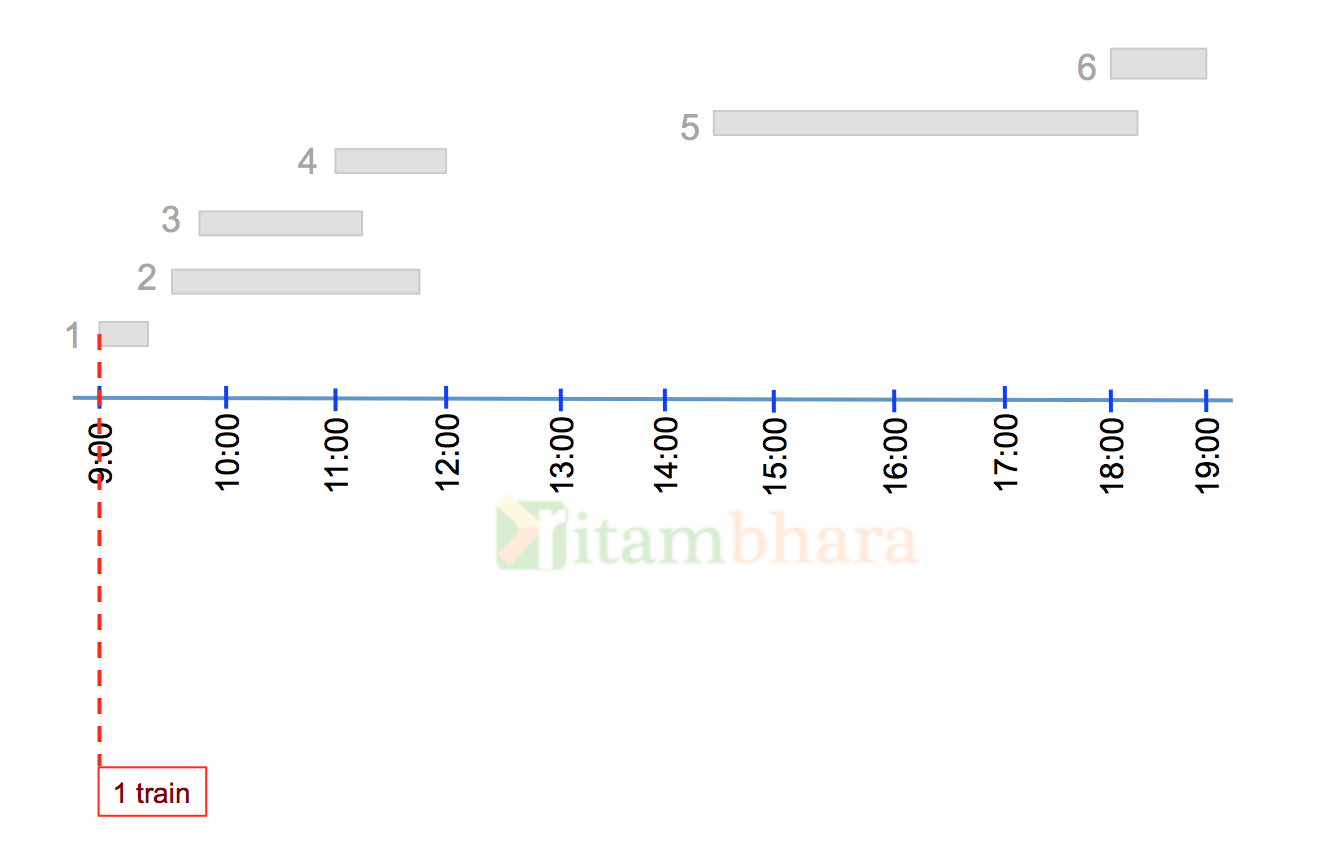
Consider all the events, be it arrival or departure as they come in the time line. The first event is at 9:00 when Train-1 arrives at the station, the total number of trains on the station at this time is one.
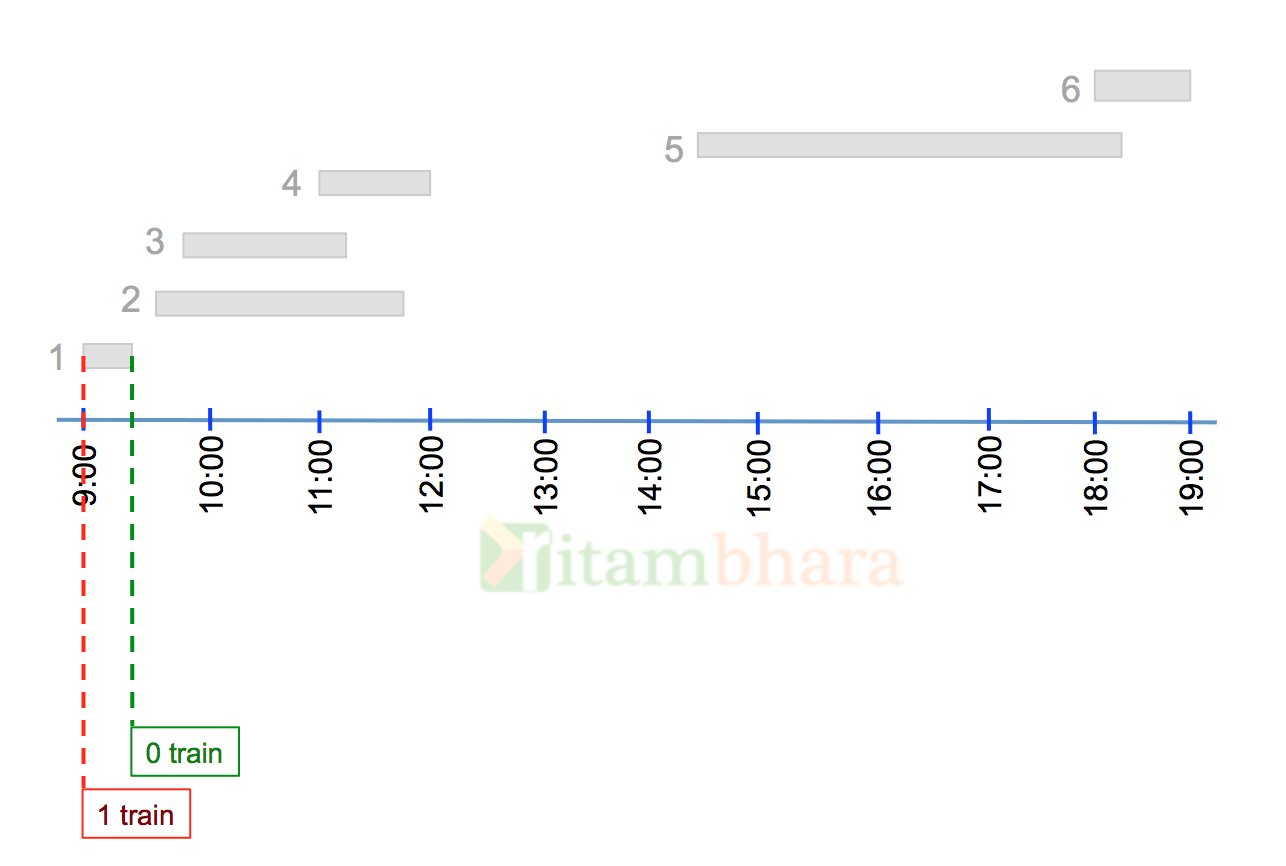
The next event is at 9:15, when this train depart, and hence the number of trains on the station becomes zero
So when a train comes, we increase the number and when a train leaves, we decrease the number of trains on the station. Going by the same logic, at 11:00 there are 3 trains on the station.
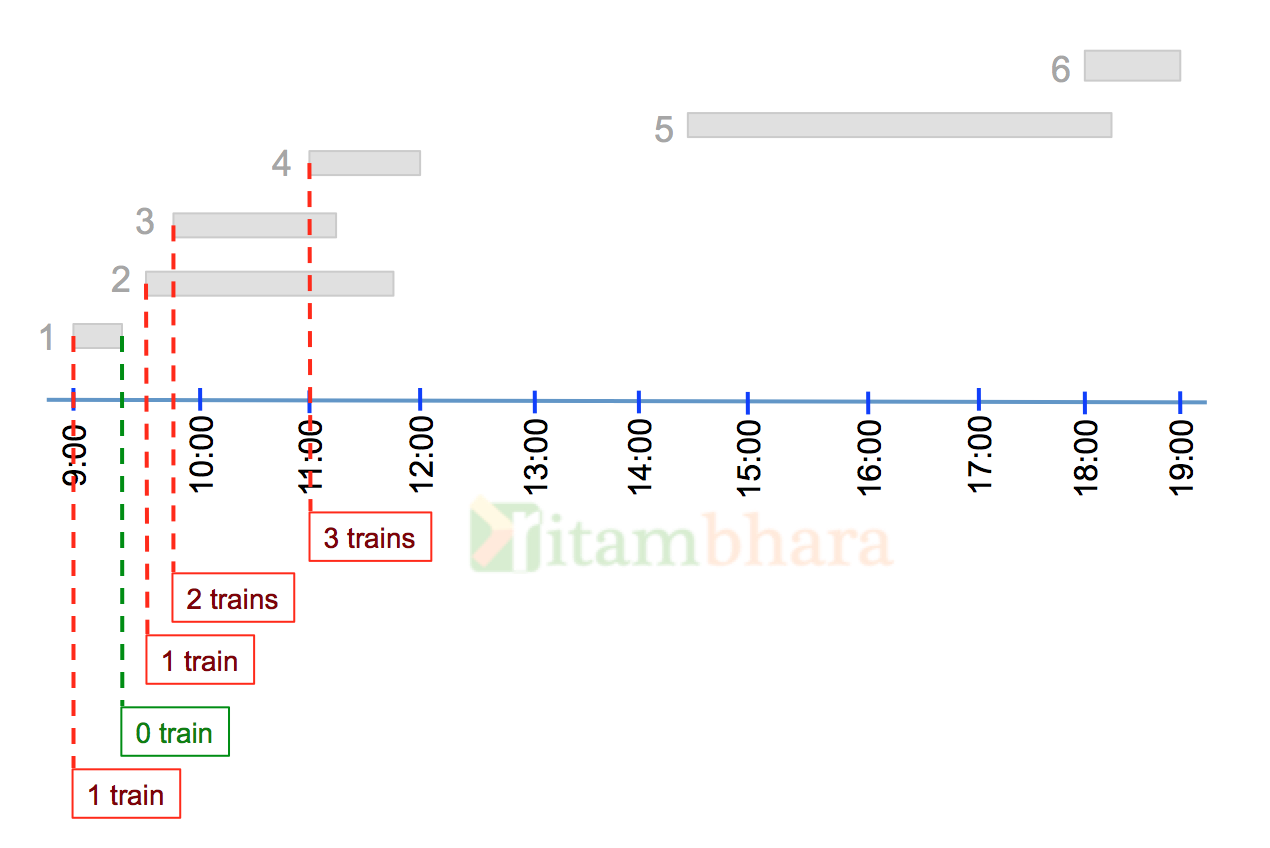
And the final picture looks like shown below:
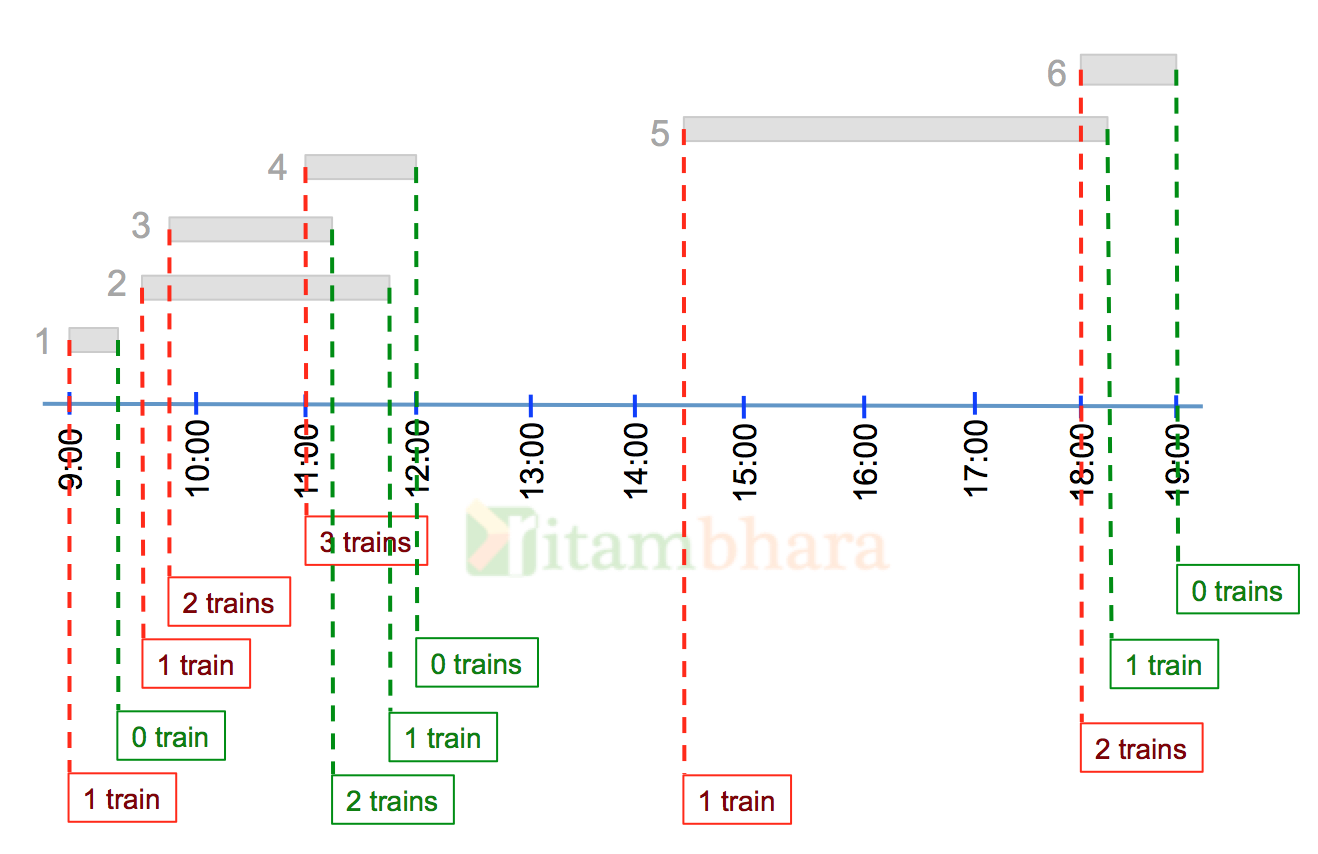
Clearly the maximum number of trains on the station at any time is 3, and it is between 11:00 and 11:05.
Code:
- Sort both the arrays holding arrival time and departure time.
- After sorting use the merging logic (without doing the actual merge). Compare the current element in arrival and departure array and pick which ever is smaller and increment the pointer of that array whose value is picked.
- If time is picked from the arrival array, increment the total number of trains on the station and if time is picked from the departure array decrease the total number of trains on the station.
- While doing the above process, we keep the count of maximum value reached till now. At the end this maximum value is returned.
Below is the code for the above logic. (You need to implement function to sort an array, or you can use the library function to do the sorting).
/**
* Calculate the minimum number of platforms required for given schedule of trains
*/
int minPlatformsRequired(double arivl[], double deprt[], int noOfTrains)
{
// Implement this function that sort two arrays or use library function.
sortArray(arivl, noOfTrains);
sortArray(deprt, noOfTrains);
int maxPlatforms = 0;
int platformsRequired = 0;
int i = 0, j = 0;
// Logic simlar to Merging of two arrays
while (i < noOfTrains && j < noOfTrains)
{
if (arivl[i] < deprt[j])
{
// New train has arrived.
platformsRequired++;
i++;
if (platformsRequired > maxPlatforms)
maxPlatforms = platformsRequired;
}
else
{
// Train left the platform.
platformsRequired--;
j++;
}
}
return maxPlatforms;
}

5 Comments
IF numberOfOverLaps > maxOverlaps THEN
numberOfOverLaps = maxOverlaps;
here reverse, i.e, maxOverlaps = numberOfOverLaps, because maxOverlpas, is zero always, if any overlaps is found numberOfOverLaps++ am i correct. and given arrays minutes > 60, like 9.75
Thanks Ravi for pointing it out. I have corrected the typo.
What if the train comes at 23.00 and leaves the next day at 00.10 ? .. wouldnt that mess up the whole algorithm. The way i see out of this is to have a function that adds 24.00 to the value if departure is less than arrival.
What are header files and output for this program?
Why do we start the inner for loop in the brute force method at i + 1