Insertion Sort
July 15, 2013Linked List Implementation of Stack in C++
July 25, 2013Number of Rectangles on a chess board
Earlier we discussed, how to calculate total number of squares (of all sizes) on the chess board. Here, the problem is, How many rectangles (of any size) will be there on the chess board?
The approach is similar to the one used in calculating the number of squares on the chess board.
Method-1: Bruit force logic
A rectangle has two sides, lets look at each rectangle on the basis of smaller side (Breadth of rectangle):
Number of rectangles having breadth = 1:
Length=1: 64 Length=2: 2 * 8 * 7 Length=3: 2 * 8 * 6 ... Length=8: 2*8*1
In fact it can be generalized for n*n board. Number of rectangles with one side as 1 will be
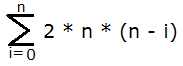
Total (with breadth=1): 64 +2*8(7 + 6 + 5 … + 1)
Number of rectangles having breadth = 2 square:
Length=2: 7*7 Length=3: 2*7*6 Length=4: 2*7*5 ... Length=8: 2*7*1
Total (with breadth=2): 49 +2*7(6 + 5 + 4 … + 1)
Similarly,
Total (with breadth=3): 36 +2*6(5 + 4 … + 1)
Total (with breadth=4): 25 +2*5(4 + 3 + 2 + 1)
Total (with breadth=5): 16 +2*4(3 + 2 + 1)
Total (with breadth=6): 9 +2*3(2 + 1)
Total (with breadth=7): 4 +2*2(1)
Total (with breadth=8): 1
The perfect squares (64, 49, 36 …) are actually the number of squares and the summation series are perfect rectangles (length and breadth not equal).
Hence, the total number of rectangles will be:
(1+4+9+16+25+36+49+64) + (1*2^2 +2+3^2 +3+4^2 +…7*8^2) = 1296
Method-2: Using Combinatorics (Combination)
There are 9 horizontal lines and 9 vertical lines. A rectangle will be formed by two vertical and two horizontal lines.
And two horizontal lines can be selected in 9C2 ways (can also be written as C(9,2))
C(9,2) = 9! / (2! * 7!)
Similarly, number of ways to select 2 lines out of 9 vertical lines is also
C(9,2) = 9! / (2! * 7!)
Total number of ways to form a rectangle will be
C(9,2) * C(9,2) = n2*(n+1)2/4 = 1296.

2 Comments
Hi,
Number of rectangles having breadth = 2 square:
Length=2: 2*2 has to be Length=2: 7*7. [Even though, in calculating the Total, it is 49]
Thanks
Krishna
Thanks Krishna for pointing it out.. I have updated the post.