Binary Search or Half-interval search
June 29, 2013Selection Sort
June 30, 2013Optimized bubble sort algorithm
 What is Bubble Sort. Write algorithm of mention the Time & Space complexity of the Algorithm. Also suggest improvements which will improve the best case running time of Algorithm to O(n).
What is Bubble Sort. Write algorithm of mention the Time & Space complexity of the Algorithm. Also suggest improvements which will improve the best case running time of Algorithm to O(n).
Solution:
Bubble Sort is a sorting algorithm which compares two adjacent elements and swap them if they are not in the right order. To sort the entire array, the array is traversed n-1 time (array having n elements). These are called passes, In the first pass the largest element moves to the last position (sorting in ascending order). So if the original (unsorted) array is:
5 2 4 3 6
then during first pass, adjacent elements will be compared, and swapped if not in order (if larger element is on left side) as shown below:
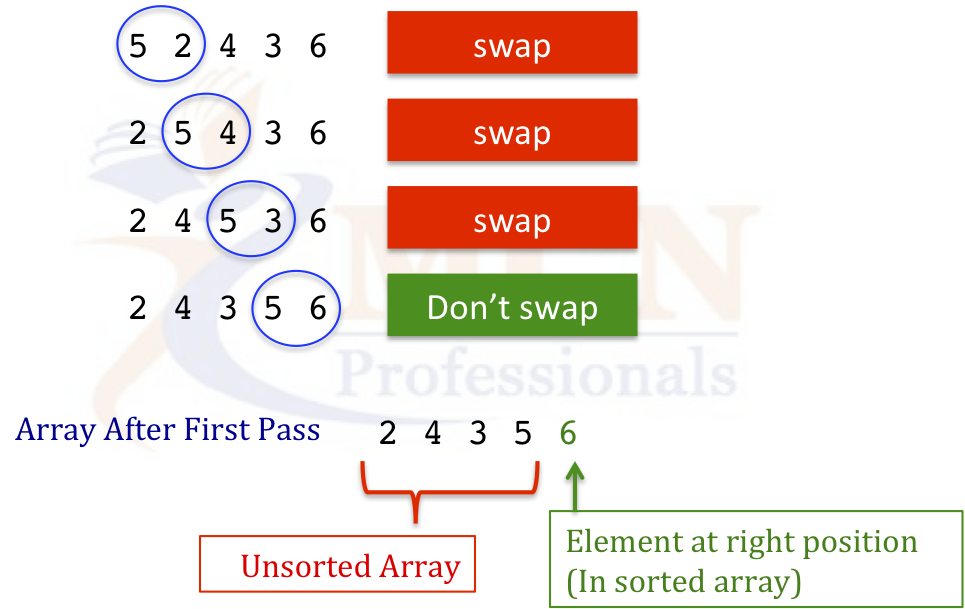
After first pass the largest element is at the last position.
Now, in the 2nd pass, we will consider the first (n-1) elements only (because last position already has largest element). After 2nd pass the array will be
2 3 4 5 6
i.e, 5 will be moved to the (n-1)th position. In the 3rd pass 3rd largest element will be moved to the (n-2)th position and so on.
After (n-1) passes, (n-1) elements will be moved to their proper positions, the last element has to be the smallest. So the array will be sorted after n-1 passes.
Algorithm:
void bubbleSort(int *arr, int n)
{
for(int i=0; i<n; i++)
{
for(int j=0; j<n-i-1; j++)
{
if(array[j]>array[j+1])
{
int temp = array[j+1];
array[j+1] = array[j];
array[j] = temp;
}
}
}
}
Time Complexity: O(n2)
Extra Space taken: O(1) – In-place algorithm.
Improvement (Optimization):
In the above example, the array got sorted after 2nd pass, but we will still continue with the 3rd, 4th pass. Suppose if the array is already sorted, then there will be no swapping (because adjacent elements are always in order), but still we will continue with the passes and there will still be (n-1) passes.
If we can identify, that the array is sorted, then we should stop execution of further passes. This is the optimization over the original bubble sort algorithm.
If there is no swapping in a particular pass, it means the array has become sorted, so we should not perform the further passes. For this we can have a flag variable which is set to true before each pass and is made false when a swapping is performed.
void bubbleSort(int *arr, int n)
{
for(int i=0; i<n; i++)
{
bool flag = false;
for(int j=0; j<n-i-1; j++)
{
if(array[j]>array[j+1])
{
flag = true;
int temp = array[j+1];
array[j+1] = array[j];
array[j] = temp;
}
}
// No Swapping happened, array is sorted
if(!flag){
return;
}
}
}
Note, that if all the passes are performed, then our optimized algorithm will in fact perform a little slower than the original one. But for the best case (Array already sorted) it will be O(n), For average case also the performance will see an improvement. Whereas the original algorithm was O(n2) for all the cases.

5 Comments
[…] https://www.ritambhara.in/optimized-bubble-sort-algorithm/ […]
best sloutions for this program
http://programmergallery.com/c-program/bubble-sort-algorith-program-using-c-program.php
[…] Source: https://www.ritambhara.in […]
[…] Source: https://www.ritambhara.in […]
[…] Source: https://www.ritambhara.in […]