Selection Sort

Selection sort is an in-place, comparison sorting algorithm. Like bubble sort it also divides the given array in two sub arrays sorted and unsorted, divided by an imaginary wall.
Initially all the elements will be in the unsorted list. Each pass will pick the smallest element from the unsorted list and add it at the end of the sorted list, this will move the imaginary wall one step forward making more room in the sorted list and less room in the unsorted list.
After i passes, there will be i elements in the sorted list and (n-i) elements in the unsorted list. Hence we need n passes to sort the entire list, But out of n passes we can skip the last pass, because if n-1 smallest elements are removed from the list, then the last element left will be by default the largest.
Example: Let the initial (unsorted) array be as given below:

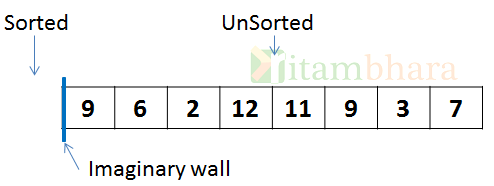
Initially all the elements are in the unsorted list. We will search for the smallest element in the unsorted list and then swap it with the first element.

Then search for the next smallest element in the sorted list and replace it with the second element.

Repeat the above process for all the element:

Once n-1 smallest elements are moved at the first (n-1) positions in sorted order, we don’t need to do anything, because the last element will be the largest. (Hence, we need to execute only n-1 passes)

Code:

void selectionSort(int *arr, int n)
{
    for(int i=0; i<9; i++)
    {
        // index of smallest element in unsorted array.
        int min = i;
        for(int j=i+1; j<10; j++)
        {
            if(arr[j]<arr[min])
                min = j;
        }
        // If first element in the unsorted list is not the smallest
        // swap it with the smallest.
        if(min != i)
        {
            int temp = arr[min];
            arr[min] = arr[i];
            arr[i] = temp;
        }
    }
}

Time Complexity: O(n²)
Extra Space used: O(1) – In place algorithm.
Comparison of Selection sort and Bubble sort:

Selection sort is almost similar to Bubble sort. The major difference is that there is only one swap per pass in selection sort where as there is no such limit for bubble sort.

The optimization of bubble sort can also be applied on selection sort. So in a way, it is more optimized than Bubble sort