Keep Body Cameras Off Public-School Educators
May 27, 20155 Pirates Puzzle dividing 1000 coins
June 21, 2015Storing Binary Tree in a file
Given a Binary tree, write two function. The first function should write the binary tree in a file and second function should read the file and should be able to construct the same binary tree.
Here writing to file is not important, the important thing is to preserve the state of the Binary tree. Think of it like converting a binary tree to a String and then given that string, construct the same binary tree.
For example, If I have an array
int arr[] = {2, 3, 1, 7, 5, 6}
I can write this array to a file one element at a time linearly, then I can read the file one element at a time and construct the same array which it was before storing to the file.
Doing the same thing for binary trees is a little difficult. For example, If I have below binary tree:
10
/ \
5 25
/
30
And I decide to write the tree in level order, then I will store it to the file in following form:
10 5 25 30
When I read the file later, I do not know, whether 30 is the child of 5 or 25, and whether it is the left child or the right child.
If our tree is of a special type, then it may be stored. For eample, it is easy to store Complete Binary trees or Almost complete binary trees in because there we don’t have gaps (nodes missing) in between at any layer, hence we can store them in level order traversal and while reading the file we know which node fits where. but this solution will not work for a normal binary tree.
Solution-1: Storing the traversals
I have discussed earlier, that we can construct the tree from traversals. But we need at least two traversals to construct the original tree (e.g if preOrder and inOrder traversals are given then we can construct the tree).
Traversing a binary tree is an O(n) time operation. we have discussed the basic tree traversals here… The above problem can be solved, as shown below:
Writing to the file
- Traverse the tree in preorder and keep writing the node to the file.
- Once the nodes are written in the file in preorder traversal. Insert a new line.
- Traverse the tree in inorder and keep writing the node to the file.
Reading from the File
- Read the first line, it is preorder of the tree
- Read the next line, it is inOrder of the tree.
- Construct the tree
Note that we cannot construct the tree from pre-order and post-order traversals. We need in-order traversal and one of the two (pre or post order).
Solution-2: Using level-order traversal
As seen above, for a complete binary tree and an almost compete binary tree, we can just store the level order traversal and construct the whole tree from that traversal.
For example, below binary tree is almost complete
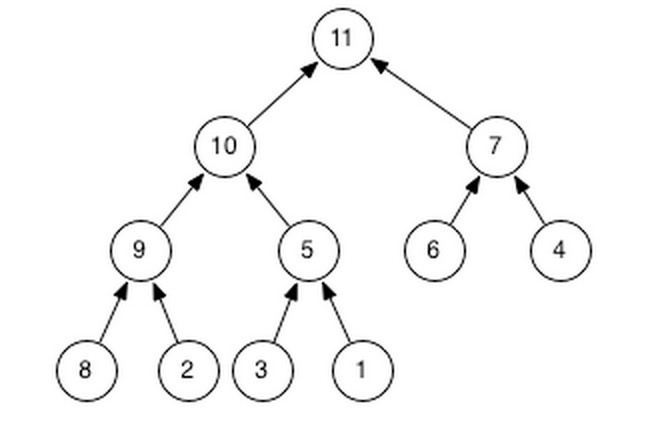
We store the level order traversal in the file
11 10 7 9 5 6 4 8 2 3 1
When we read from the file, being a binary tree, we know that first element is root, then next 2 elements are from level-1, next 4 elements from level two and so on… hence we can easily construct the tree.
But given tree is neither complete nor almost complete. So there may be missing nodes in between, for example, in the below binary tree left child of 30 is missing.
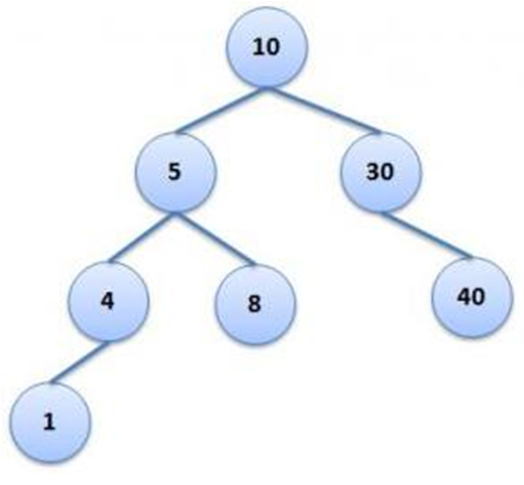
In this case, we will store some value (say, -1) to indicate the missing node. If we know that all the values in the tree are positive integers and we store -1 for all the absent node in the tree, then, for the above tree, we will save the following data in the file
10 5 30 4 8 -1 40 1 -1 -1 -1 -1 -1 -1 -1
Note that we are considering all the places where a node would have been had the above tree been a complete binary tree. If the above tree is complete binary tree then it will look like below:
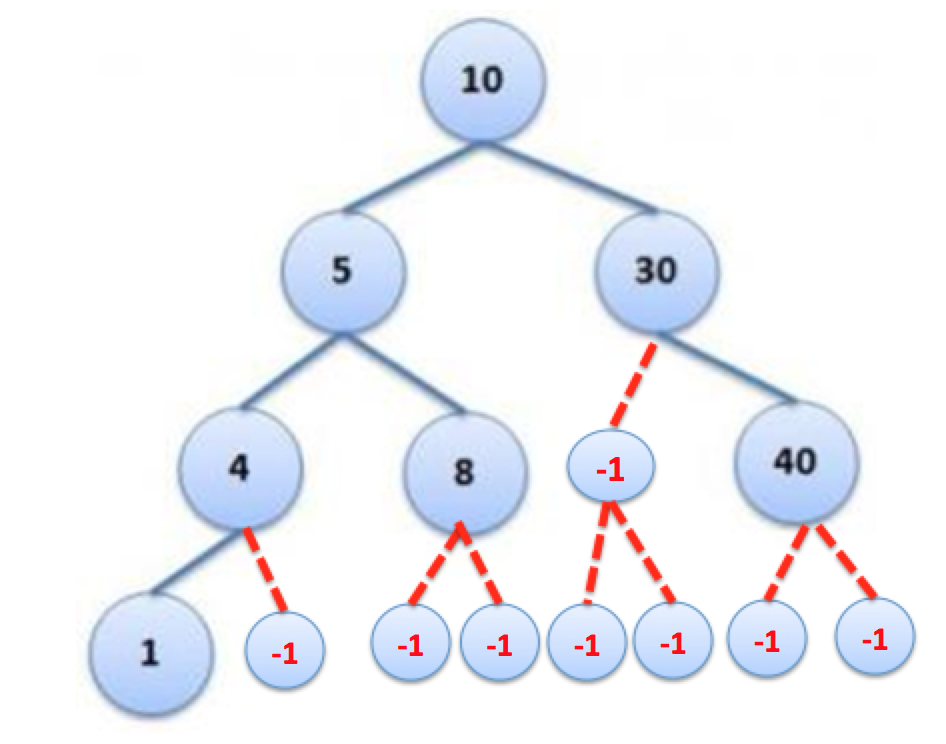
The nodes with -1 are smaller because there is less space, and not because they are special.
Now, when we read back from the file, we will just skip creating nodes corresponding to -1 values in the file. And we will get the same tree back.
Code
Below is the code for above logic. In the below code we are writing the tree to an array, rather than storing it to file. It is only because reading/writing to file will make the code unnecessarily complex. Start reading the code from the main function. It is first constructing the tree, then storing that tree in an array (with -1 values corresponding to missing nodes), and finally it is constructing the tree from that array. This new tree should be exactly same as the previous one.
#define EMPTY_SPACE -1
struct Node
{
int data;
Node* lptr;
Node* rptr;
Node(char value): data(value), lptr(NULL), rptr(NULL){}
};
// It is needed to calculate the size of array.
int heightOfTree(Node* root)
{
if(root == NULL)
return 0;
else
return max(heightOfTree(root->lptr), heightOfTree(root->rptr)) + 1;
}
// Traverse the tree in inorder and keep storing
// each node at right place in the array arr.
// Initial value of pos is 0
void populateNodesInArray(Node* r, int* arr, int pos)
{
if(r == NULL){ return; }
arr[pos] = r->data;
if(r->lptr != NULL){
populateNodesInArray(r->lptr, arr, 2*pos + 1);
}
if(r->rptr != NULL){
populateNodesInArray(r->rptr, arr, 2*pos + 2);
}
}
void treeToArray(Node* root, int* arr, int maxNodes)
{
// Initialize all the nodes with -1
for(int i=0; i<maxNodes; i++)
arr[i] = -1;
// Populating nodes in array
populateNodesInArray(root, arr, 0);
}
// pos is the position of root in array
void populateTreeFromArray(Node* r, int* arr, int n, int pos)
{
if(r == NULL || arr == NULL || n==0){ return; }
// Setting the left subtree of root
int newPos = 2*pos+1;
if(newPos < n && arr[newPos] != EMPTY_SPACE)
{
r->lptr = new Node(arr[newPos]);
populateTreeFromArray(r->lptr, arr, n, newPos);
}
// Setting the Right subtree of root
newPos = 2*pos+2;
if(newPos < n && arr[newPos] != EMPTY_SPACE)
{
r->rptr = new Node(arr[newPos]);
populateTreeFromArray(r->rptr, arr, n, newPos);
}
}
// We will discard all the negative values as empty spaces
Node* arrayToTree(int* arr, int n)
{
if(arr == NULL || arr[0] == EMPTY_SPACE){ return NULL; }
// We will populate the root node here
// and leave the responsibility of populating rest of tree
// to the recursive function
Node* root = new Node(arr[0]);
populateTreeFromArray(root, arr, n, 0);
return root;
}
// Helper function to print the tree in PreOrder
void preOrder(Node* r)
{
if(r==NULL){return;}
cout<data << " "; preOrder(r->lptr);
preOrder(r->rptr);
}
// Helper function to print the tree in InOrder
void inOrder(Node* r)
{
if(r==NULL){return;}
inOrder(r->lptr);
cout<data << " "; inOrder(r->rptr);
}
// Helper function to print values of the array
void printArray(int* arr, int n)
{
cout<<"\nArray is : ";
for(int i=0; i<n; i++)
{
cout<<arr[i]<<" ";
}
cout<<endl;
}
int main()
{
// Constructing the tree
Node* r = new Node(10);
r->lptr =new Node(5);
r->rptr=new Node(30);
r->lptr->lptr = new Node(4);
r->lptr->lptr->lptr = new Node(1);
r->lptr->lptr->rptr = new Node(8);
r->rptr->lptr = new Node(40);
int height = heightOfTree(r);
// Max number of nodes possible of this height.
// is 2^height - 1
int maxNodes = (1<<height) - 1;
int *arr = new int[maxNodes];
cout<<"Inorder Traversal of tree: ";inOrder(r);
cout<<"\nPreOrder Traversal of tree: ";preOrder(r);
treeToArray(r, arr, maxNodes);
printArray(arr, maxNodes);
Node* newTree = arrayToTree(arr, maxNodes);
cout<<"Inorder Traversal of tree: ";inOrder(newTree);
cout<<"\nPreOrder Traversal of tree: ";preOrder(newTree);
return 0;
}

1 Comment
Pls for the code to store the tree travesal on a file