Storing Binary Tree in a file
June 18, 2015Count all left nodes in a Binary tree
June 24, 20155 Pirates Puzzle dividing 1000 coins
There are 5 pirates, A, B, C, D and E. They have a strict hierarchy, A is senior to B, B is senior to C, C is senior to D and D is senior to E. So it is like (A > B > C > D > E).
These pirates have 1000 gold coins which they want to distribute among themselves. The rules of distribution is as follows:
- The most senior pirate should propose a distribution. - All the pirates (including the most senior) will vote on whether they accept the distribution or not. - If half or more pirates vote in the favour of distribution, then distribution is accepted and game ends. - If more than half votes against the distribution, then the senior most pirate will be killed and the next senior most will propose a new distribution and this will continue.
When a pirate vote, they make their decision based on three factors (in this order):
- First of all, each pirate want to survive.
- Second, given survival, each pirate want to maximize the number of gold coins he gets.
- Third, given a situation of no-gain no-loss, each pirate would prefer to kill the other pirate.
Considering that all pirates are very strong in logic, and if a logic can be deduced, then they will deduce it. How should A distribute the coins so that he does not get killed and also gets the maximum coins possible.
Solution:
Intuitively it may appear that A will have to give most of the money (if not all) to the junior pirates so that his life can be saved. But that will not work.
Suppose, If A decide to distribute 250 coins to each B, C, D and E and keeps nothing for himself, then also he will be killed, because all others will vote against him, they can get the same distribution even if A is killed, and pirates want other pirates to be killed.
So, finding a solution like this is very difficult. The solution to such puzzles can be easily found working in the bottom-up manner:
1. If there is just one pirate, say E then the distribution is very easy. He keeps everything to himself
![]()
2. If there are 2 pirates, say D and E (D senior to E), then D will distribute the coins like:

D will vote in favour of his distribution and the distribution will be accepted (because half people voted in favour).
3. If there are 3 pirates, C, D, and E (C being senior most), then C will make the following distribution:
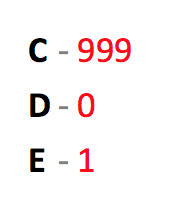
Now, C will obviously vote in favour. E knows that if C dies then D will make the next distribution and he will get nothing (see the distribution above for 2 pirates), hence E will also vote in favour (because they want to maximize their profit). And the distribution is accepted (2 votes in comparison to 1 vote)
4. If there are 4 pirates, say B, C, D, E. Then B will make the following distribution:

Now, B and D will vote in favour of this distribution, because, If the distribution is not accepted and B dies, then C will have to make the distribution, and D will get nothing (see the distribution when there are 3 pirates above). Hence because 50% pirates voted in favour of distribution, it will be accepted.
5. Now, If there are 5 pirates, A, B, C, D and E. Then A will make the following distribution:
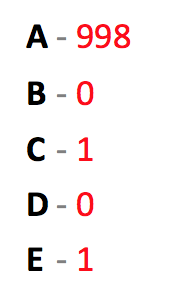
By the same logic, A, C and E will vote in favour of the distribution and hence the distribution will be accepted.
Now if the question is asked for 6 pirates, then you can answer similarly. In fact we can find the solution for any number of pirates.
Can you write a code for it? the function will receive the number of pirates and coins and it should print the total number of coins each pirate should get ? Try it out 🙂

2 Comments
Interesting puzzle. 🙂
what will be the java code?