Recursive implementation of Insertion Sort
May 28, 2017Next greater element
June 28, 2017Introducing Graph Data Structure with Adjacency matrix implementation
Binary tree is a specialization of Graph data structure. Node in a Graph is called a Vertex and the connection between two vertices is called an Edge.
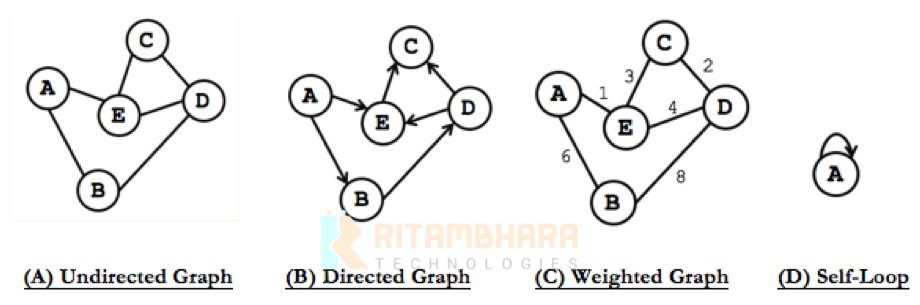
If we use this terminology, A Binary tree edge is only from a parent to its (at the most two) children. In Graph, any vertex (Node) can connect to any vertex and there is no limit on the number of vertices that a vertex can connect to. The connection can be uni-directional (as in Binary trees) or bi-directional. When connections are uni-directional the edge is called directed edge and graph is called directed graph. When connections are bi-directional, edge is called un-directed edge and graph is called undirected graph. Because of these connections, there is no hierarchy among the vertices of a Graph.
Graph is a very good data structure to simulate real-life connections. Consider the connection between cities. Represent every city with a vertex and the road connecting two cities as an edge between them. Every edge can have a weight, that represent length of the road.
It is not practical to represent Graph like Binary trees using Node structure.
There are two major representations of graph in computers. Adjacency Matrix and Adjacency list. The first one is discussed in this post.
Adjacency-Matrix Implementation
In adjacency matrix implementation, a two-dimensional array is taken of order N*N, where N is the number of vertices. The cell (i,j) is true if there is an edge from Vertex-i to Vertex-j or if Vertex-i and Vertex-j are adjacent. For the undirected graph shown in Figure 0.2(A) the adjacency matrix looks like:
| A | B | C | D | E | |
| A | 0 | 1 | 0 | 0 | 1 |
| B | 1 | 0 | 0 | 1 | 0 |
| C | 0 | 0 | 0 | 1 | 1 |
| D | 0 | 1 | 1 | 0 | 1 |
| E | 1 | 0 | 1 | 1 | 0 |
False is represented by a 0 and true by a 1. Because each cell stores a binary value, we can save space by using a bit-matrix. When graph is weighted graph (each edge has a weight) cells may store weight of the edge, with 0, representing absence of edge as shown below.
| A | B | C | D | E | |
| A | 0 | 6 | 0 | 0 | 1 |
| B | 6 | 0 | 0 | 8 | 0 |
| C | 0 | 0 | 0 | 2 | 3 |
| D | 0 | 8 | 2 | 0 | 4 |
| E | 1 | 0 | 3 | 4 | 0 |
The above matrix is symmetric and diagonal elements have no meaning. This is a fit case of using a sparse matrix to save memory. When the graph is directed, then we have to keep the complete matrix.
There are two most used functions in a graph:
- Given two vertices, check if they are connected or not .
- Given a vertex, print all its adjacent vertices .
The vertices are complex structures, in our example, a vertex represent a city, we may have lot of information around the city (like name, population, socio-economic indices, etc.). To simulate a real life situation, we can keep the vertex array separate from the adjacency matrix.
char vertex[N] = {'A', 'B', 'C', 'D', 'E'};
int edges[N][N] = { {0, 1, 0, 0, 1},
{1, 0, 0, 1, 0},
{0, 0, 0, 1, 1},
{0, 1, 1, 0, 1},
{1, 0, 1, 1, 0} };
Cell edge[i][j] represents connection between vertex[i] and vertex[j]. We have decoupled the vertex information from connections. This decoupling is important because if my computer is connected to a network, changing computer name does not affect connection, because vertex-id does not change. The index of vertex can be used as vertex-id. Below function receives a vertex and return vertex-id of that vertex
int getVertexId(char v)
{
for(int i=0; i<N; i++)
if(vertex[i] == v)
return i;
return -1;
}
Function isAdjascent returns true if the two vertices are connected and false otherwise.
bool isAdjascent(char v1, char v2)
{
int i = getVertexId(v1), j = getVertexId(v2);
// INVALID VERTEX
if(i == -1 || j == -1) { return false; }
return edges[i][j];
}
If getVertexId function is implemented as a constant-time function (using hash) then isAdjascent function takes constant time. This is the biggest advantage we get with adjacency matrix implementation. Below code print all adjacent nodes for a given vertex
void printAllAdjescent(char v1)
{
int i = getVertexId(v1);
if(i == -1){ return; } // INVALID VERTEX
for(int j=0; j<N; j++)
if(edges[i][j] != 0)
printf(" %c", vertex[j]);
}
This function traverse the entire row and takes O(N) time. In a directed graph, an edge can be from a vertex to itself, this is called self-loop.
