Coin heap puzzle
May 12, 2016Binary Heap
June 19, 2016Almost complete Binary Tree
A complete Binary tree of height h has 2h-1 nodes. Out of these 2h-1 are leaf nodes and rest (2h-1-1 are non-leaf. Read more about complete binary trees here or watch video. Below are all complete binary trees:
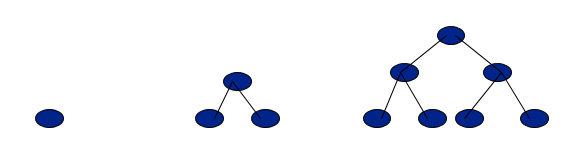
[rapid_quiz question=”All Leaf nodes of complete binary tree are at same level ” answer=”yes” options=”yes|no” notes=”There is no hole in complete binary tree. It has maximum number of nodes possible for any binary tree of a particular height”]
[rapid_quiz question=”In complete binary tree, there will never be a node that has only one child and the other child is NULL” answer=”yes” options=”yes|no” notes=”All non-leaf nodes will have both the children.”]
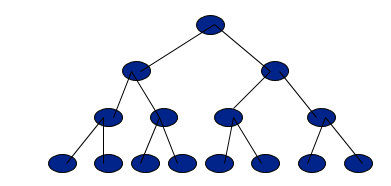
None of the below trees is complete binary tree:
Canonical labeling of nodes
Label the Nodes in the level-wise fashion from left to right, as shown below:
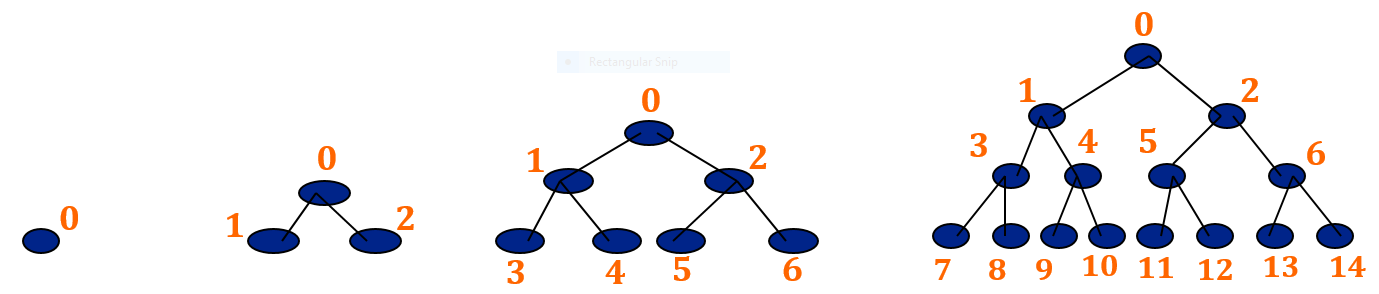
The advantage of canonical labeling is that such a tree can be stored in an array where value of a node is stored at the index equal to its label in the tree.
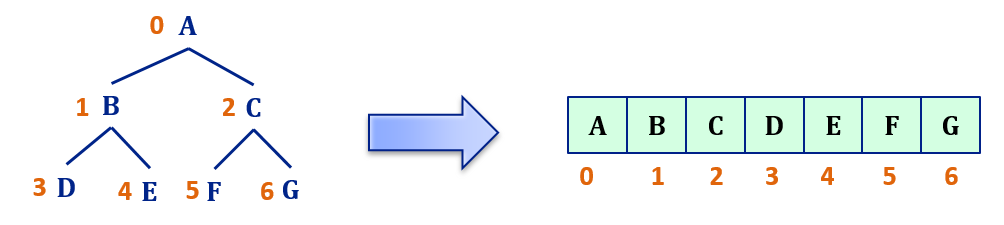
This way we will save a lot of memory because we do not need to store all the pointers. If you have noticed, there is a relationship between the labels of a node and its children above:
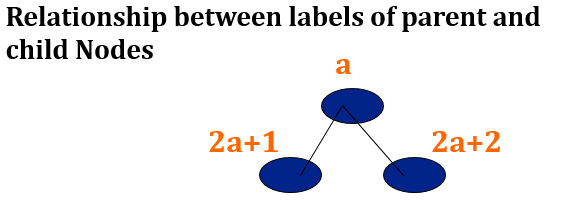
This way, it becomes easy to move in either upward or downward direction of a tree, even when it is stored in an array.
Almost Complete Binary Tree
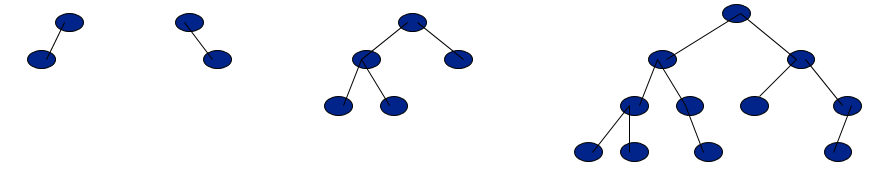
A the binary tree made up of the first n nodes of a canonically labeled complete Binary Tree is called Almost complete Binary Tree. Below are all almost complete binary trees,

Below trees are NOT almost complete binary trees (the labeling has no meaning, because there are gaps).
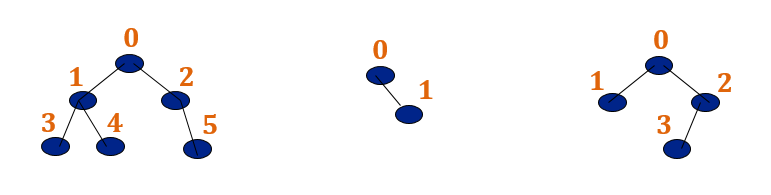
As seen above an almost complete binary tree can be stored in an array.
[rapid_quiz question=”Every almost complete binary tree is also ‘Complete Binary tree'” answer=”True” options=”True|False” notes=””]
We have earlier written code to check is a given tree is an Almost complete binary tree or not.

4 Comments
A complete Binary tree of height h has ((2 to the pow of h)-1) nodes is wrong. This property is true for full binary tree.
*A complete Binary tree of height h has atleast (2 to the pow of h-1) nodes and atmost ((2 to the pow of h)-1) nodes
1. All Leaf nodes of complete binary tree are at same level – False
2. In complete binary tree, there will never be a node that has only one child and the other child is NULL – False
Kamal Rawat Agreed
Kamal Rawat Agreed