Birthday Paradox (Birthday Problem)

You may solve the simple probability, “Given a set of n randomly chosen people, what is the probability of two people having same birthday?”
You may also solve,  “At least how many people need to be picked to make the probability 100% that at least two of them have same birthday?”

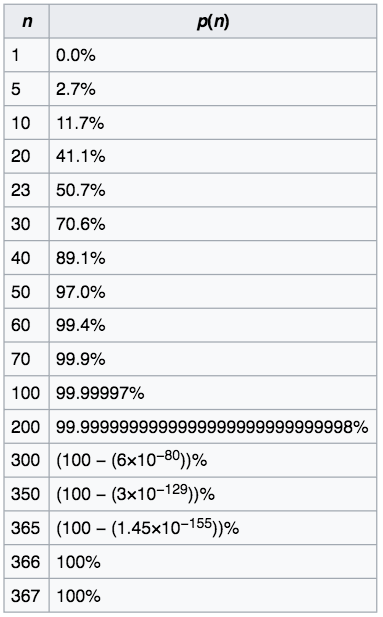
Answer to the second question is 367, because there are 366 possible birthdays (including Feb-26).

The question now is, “At least how many people need to be picked to make the probability 99.9% that at least two of them have same birthday?”

Answer is 70.

And if the question is,“At least how many people need to be picked to make the probability 50% that at least two of them have same birthday?”

Answer is 23.

Let us first the first question,“Given a set of n randomly chosen people, what is the probability of two people having same birthday?”
If P is the probability then P’ is the probability of no two people (out of n) have the same birthday.
P = 1 – P’
P’ can be calculated as below

For 23 people, this comes out to be

P’ = 1 * (364/365) * ( 363/365)*… * (343/365)

Solving the equation, we get

P’ = 0.492703

P = 1-P’ = 0.5 (approx)

For different values of n, following are the probabilities:

(Refer: https://en.wikipedia.org/wiki/Birthday_problem)

Please refer the above link to see how to derive n from probability.