Check if a subtree exist with a given sum

Given a binary tree and a Number N, write code to check if there exist a subtree of the Binary tree with sum of all the nodes = N.

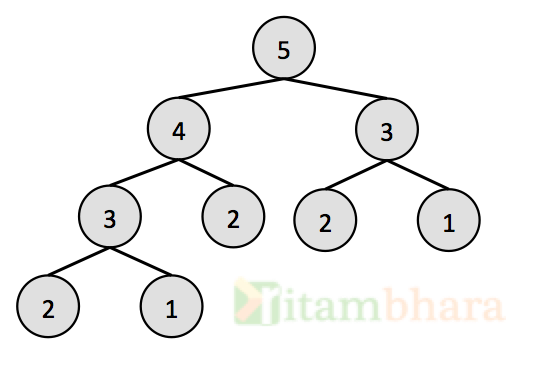
For example, if the Binary tree is as given on the right:
And N = 12, then the output should be ‘true’ because there exist a subtree (with root at Node-4), for which sum of all the nodes is 12 (4+3+2+2+1).

Solution:

Tree questions are usually solved using recursion. In this case also we solve it using recursion.
As in most Binary tree questions, we first decide on the traversal. In this case it makes sense to traverse the tree in post-order traversal.
while post traversing we know that,

sum of current subtree = sum of left subtree + sum of right subtree + value of current node

We keep checking if this sum is equal to N or not.
Since we require to return two values, the sum of current subtree and whether or not it a subtree exist with sum ==N. we use pass-by-reference to pass this second value.

// MAIN FUNCTION TO CHECK IF THERE EXIST A SUBTREE WITH SUM = N
// curSubtreeSum - Variable populated by this function
// r - ptr to the root of the tree
bool subTreeWithSumRec(Node *r, int *curSubtreeSum, int n)
{
  // TERMINATING CONDITION
  if (r == NULL){
    *curSubtreeSum = NULL;
    return false;
  }
  int leftSubTreeSum = 0;
  bool leftExist = sumSubtreeUtil(r->left, &leftSubTreeSum, n);
  int rightSubTreeSum = 0;
  bool rightExist = sumSubtreeUtil(r->left, &rightSubTreeSum, n);
  *curSubtreeSum = leftSubTreeSum + rightSubTreeSum + r->data;
  return ( leftExist || rightExist || *curSubtreeSum == n));
}
// WRAPPER FUNCTION (to call main function)
bool subTreeWithSum(struct Node *root, int sum)
{
    int temp = 0;
    return subTreeWithSumRec(root, &temp, sum);
}

The above code takes O(n) time, where n is total number of nodes. This is same as time taken by post-order traversal.
To further optimize the time, we can have a check that if leftExist is true, then return from there itself, rather than computing rightExist by calling the function again recursively.