Check if two arrays are permutation of each other
June 27, 2015Points on globe – Interview puzzle
June 29, 2015Fastest horse Interview question
There are twenty five horses and you can conduct a race of only five horses at one time. There is no way to find out the absolute speed of a horse (we only know there relative speed).
At least how many races will it take to determine the three fastest horses?
This is a typical interview question that uses tournament method. Since there is only one track where only 5 horses can run.
Brute-Force solution (wrong)
The brute-force approach will have 12 races as shown in the below diagram (Circle represent a race):
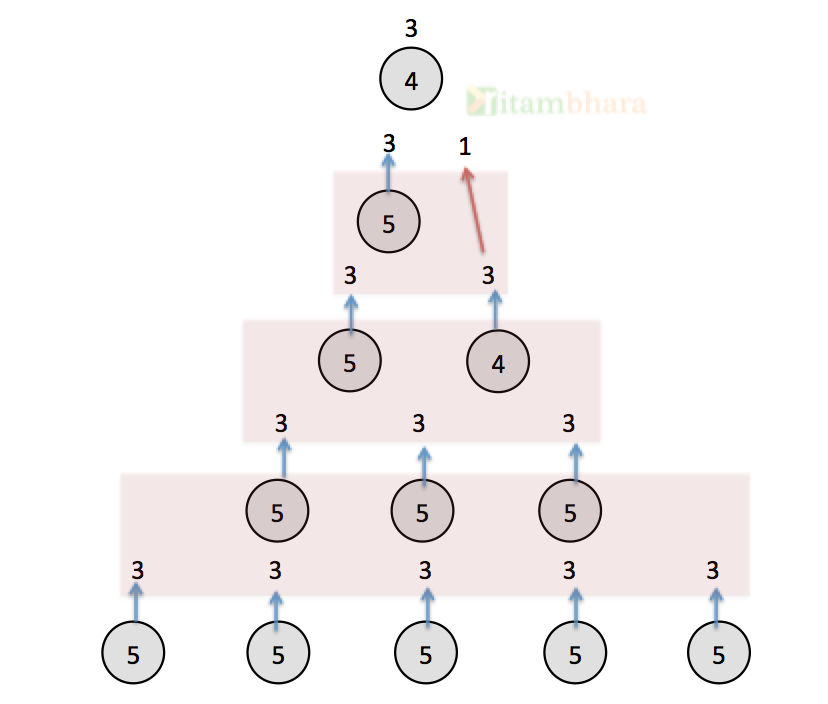
Since only 5 horses can run at one time, divide the horses in a group of five, we will have five different groups of horses. A race will be conducted separately for each group which will help us find the top three horses from each race.
After this first round (of 5 races) we have 15 horses. Now, divide them in three groups of five horses each and conduct 3 races…
Continue like that.. after the third round, we will have six horses, at this point conduct the race of 5 horses and leave one spare horse to be considered in the next round (denoted by red arrow).
Optimised (Right) Solution
Obviously the above solution is not optimised. In the most optimised solution, we need just seven races as shown below:
1. Divide the horses in 5 groups of five horses each and have 5 races (as in brute-force approach). But from each race pick only the top horses.
This way we will have 5 horses, run these five horses to get the fastest horse.
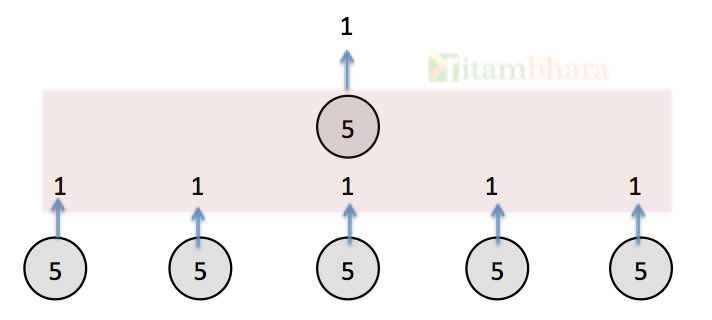
We have 6 races till now. You must know the relative order of each horse in all the races.
At this point, we know that fastest horse among all the horses. Now, we need to find the second and third fastest horses.
The second fastest is the one who is being defeated by the fastest horse. There are 2 such horses:
- The horse that came second in the 6’th race.
- The horse which was defeated by the fastest horse in first round. For example, if the winner of third race became the ultimate winner (after 6’th race), then the horse which came second in the third race.
Similarly, the third fastest horse has to be one of the following:
- The horse which came third in the 6’th race.
- The horse which came third in the race of first round that involves fastest horse of 6’th race.
- The horse which came second in the race of first round that involves the 2’nd fastest horse of 6’th race
From the above discussion we have 2 horses one of which has to be the second fastest, and three horses out of which is third fastest. We run these 5 horses in a race and pick the top two horses as second and third fastest horses.

4 Comments
I don't have optimal solution right now but I see flaw in the optimal solution; what if 3rd horse from 2nd fastest horse's group is faster than fastest horse's 2nd horse?
We need to cater to below 3 Scenarios for the optimal solution:
1. All top 3 horses are from same group
2. All are from different groups
3. 2 are from one group and they can be:
A) 1st and 2nd from same group
B) 1st and 3rd from same group
C) 2nd and 3rd from same group
I think these cases are being taken care of:
1. While finding the 2nd fastest horse we consider the horse that came 2nd in first round of race involving the fastest horse. While finding the 3rd fastest horse we consider the horse that came 3rd in the first round of race involving the fastest horse.
2. All top horses from each group actually move to 6'th race. So they are all taken care of.
3. A) In this case 3rd horse has to be the one which came 2nd in the 6'th race.Hence being taken care of.
3. B) In this case 2nd horse has to be the one which came 2nd in the 6'th race (because he has beaten the toppers from each group).Hence being taken care of.
3. C) In this case the 2nd horse is the one which came 2nd in the 6'th race. and we did consider the horse defeated by this horse in the first round/
I think, the cases that you were enumerating over phone are all taken care of.. or is there anything that is left ?
You mean to say that the 2nd horse from the group of 2'nd fastest horse (because the third horse from this group can only come at 4'th position – at least the fastest is at top)
This horse (which came 2nd in first round of 2'nd fastest horse) is being taken care of while considering the 3rd position.