Find kth element in union of two arrays

Given two sorted arrays of size m and n respectively. Find the k^th element in the merged result of A and B. For example, If the inputs (A, B & K ) are as given below

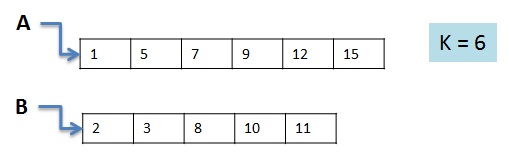
Then the merged result of the two arrays will be

And the 6th (K’th) element  = 8

Method-1: Merge the 2 arrays into 3rd one

1. Let the two arrays be A & B of size m & n respectively
2. Allocate array C of size (m+n)
3. Merge the two arrays A & B in C
4. return the k'th element of C

Code:

    /** Given two arrays a & b of sizes m & n respectively.
     * This function allocates another array (c) of size (m+n)
     * Merge the two arrays in C and return thek'th element of c.
     */
    int findElement(int *a, int *b, int m, int n, int k)
    {
        int *c = new int[m+n];
        int i=0, j=0, p=0;
        // Merging the two arrays into C
        for(; i<m && j<n; )
        {
            if(a[i] < b[j])
                c[p++] = a[i++];
            else
                c[p++] = b[j++];
        }
        if(i<m)
            while(i<m)
                c[p++] = a[i++];
        else
            while(j<n)
                c[p++] = b[j++];
        // Storing the result in a variable
        // because we need to deallocate C-array
        int elementToReturn = c[k];
        delete[] c;
        return elementToReturn;
    }

Time Complexity: O(n+m)
Extra Space used: O(m+n)

It can be further optimized, we don’t need to merge the two arrays completly. We just want the k^th element. Once we have reached the k position we can stop the further merging.

For this we just need a count variable and increment it in the merge loop. Once the value of count becomes equal to k we can stop further merging. The time complexity for this will be O(k). So if k=0 or 1 then it will take O(1) time (Best case). If k = (m+n) then it will take O(m+n) time (Worst case).

Method-2: Merging logic without extra array.

 In the above method. We actually does not need an extra array C to merge. Because we don’t want the merged result of two arrays.

What we actually want is the element at k’th position in the merged array, and NOT the entire merged array. So we just need pointers in the two arrays and a count to tell us how close we are to k’th position.

Code:

    int findElement2(int* a, int* b, int m, int n, int k )
    {
        if (k<0 || k >= m + n)
            return -1;
        int i = 0, j = 0;
        int count = 0;
        while (true)
        {
            if(i >= m)    // Array a exhausted
                return b[j+k-count];
            if(j >= n)    // Array b exhausted
                return a[i+k-count];
            if(a[i] < b[j])
            {
                if(count == k)
                    return a[i];
                i++;
            }
            else
            {
                if(count == k)
                    return b[j];
                j++;
            }
            count++;
        }
    }

Time Complexity: O(k) = O(m+n) in worst case
Extra Space Used: O(1)

Method-3: O(lg(m) + lg(n))

The above algorithm takes linear time. It is not taking the advantage of Binary search and hence can be further improved. The idea is to reduce the search sace by half in each iteration and hence reducing the elements to be searched from (m+n) to (m/2 +n/2) in the first iteration.

This will give us a Time Complexity of O(lg(n) + lg(m))

Let’s try the code… I will update it tomorrow.