Node with maximum value in a Binary search tree
July 30, 2012Find height of the Binary Tree
July 31, 2012Level of node in a Binary Tree
Given a Binary Tree and a pointer to the Node in that tree. Write a function to find level of Node in the Tree. For Example, in the below tree
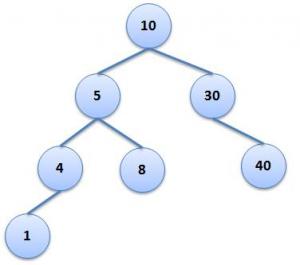 |
In the Tree on left side:
Root Node (Node with value 10) is at level-0 Nodes with values 5 and 30 are at level-1 Nodes with values 4, 8 and 40 are at level-2 Node with value 1 is at level-3 |
Signature of the function is:
/** Function returns the level of Node pointed to by ptr, in the Binary Tree
* pointed to by root.
*
* If the Tree is NULL or the Node is not present in the tree,
* then it returns -1 (Invalid level).
*/
int findLevel(Node* root, Node* ptr)
Structure of the Node is:
struct Node
{
int data;
Node *lptr;
Node *rptr;
};
Method-1 (Using Recursion):
Start at the Root with level=0 If ptr == root pointer return level Else Call the function recursively for left subtree and right subtree
Code:
/** Function returns the level of Node pointed to by ptr, in the Binary Tree
* pointed to by root.
*
* If the Tree is NULL or the Node is not present in the tree,
* then it returns -1 (Invalid level).
*/
int findLevel(Node* root, Node* ptr, int level=0)
{
if(root == NULL)
return -1;
if(root == ptr)
return level;
// If NULL or leaf Node
if(root->lptr == NULL && root->rptr == NULL)
return -1;
// Find If ptr is present in the left or right subtree.
int levelLeft = findLevel(root->lptr, ptr, level+1);
int levelRight = findLevel(root->rptr, ptr, level+1);
if(levelLeft == -1)
return levelRight;
else
return levelLeft;
}
Method-2: Using BFS
In this case we use the BFS (Breadth First Search Algorithm) which is the same algorithm we used to traverse the tree in level wise order.
Traverse the tree in level-wise order Keep a track of the level of the node. when a Node equal to ptr is encountered, return the level. If the tree is exhausted and the Node is not found return -1
Code:
<Will Update in 1 day, tomorrow>
Please let me know your comments.

2 Comments
In the findlevel function, we can check if the value of the ptr is than value of root ptr and accordingly we can traverse left or right tree and not both as its being done in this function.
Also its not very easy to write comments in this website as home/end keys are disabled and the mouse clicks are also disabled in the comment section.
good