Check if a subtree exist with a given sum
January 30, 2017Vertical distance of a Node from root
January 31, 2017Max value node between two elements of BST
Given an array of integers that represent values of nodes in a Binary Search Tree. For example, If the given array is
{9, 4, 17, 6, 5, 3, 7, 22, 20}
Then BST created from above array will be as below
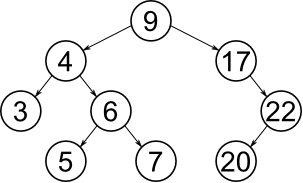
Two numbers are given (along with the array), find largest number in the path between these two numbers in the BST.
For example, if above array is given and the two numbers are 4 and 20, the max number in the path from 4 to 20 is 22.
Solution:
Let the two given numbers are a and b. The max element can be found in a two-step process:
- Find Lowest Common Ancestor(LCA) of the two nodes.
- Find the node with maximum value between LCA and greater of a and b.
The LCA of a and b is the node for which a and b does not belong to the same side.
Node * findLCA(Node* r, int a, int b)
{
// Finding the LCA of Node a and Node b
while ((a < r->data && b < r->data) ||
(a > r->data && b > r->data))
{
// IF both a and b are on the LEFT side.
if (a < r->data && b < r->data)
r = r->left;
// IF both a and b are on the RIGHT side.
else if (a > r->data && b > r->data)
r = r->right;
}
}
Once we have found the node that is the LCA. We need to find the max node in the path from LCA to a (or b, whichever is larger) using logic similar to this post.
// Return maximum element between root
// and a node in BST.
int maxElementInpath(Node *r, int x)
{
int maxElement = r->data;
// Traversing the path between ansector and
// Node and finding maximum element.
while (r->data != x)
{
maxElement = max(maxElement, r->data);
if (r->data > x)
r = r->left;
else
r = r->right;
}
return getMax(maxElement, x);
}
Below is the complete code
// Return maximum element between root
// and a node in BST.
int maxElementInpath(Node *r, int x)
{
int maxElement = r->data;
// Traversing the path between ansector and
// Node and finding maximum element.
while (r->data != x)
{
maxElement = max(maxElement, r->data);
if (r->data > x)
r = r->left;
else
r = r->right;
}
return getMax(maxElement, x);
}
int maxInPath(Node *r, int a, int b)
{
// Finding the LCA of Node a and Node b
while ((a < r->data && b < r->data) ||
(a > r->data && b > r->data))
{
// IF both a and b are on the LEFT side.
if (a < r->data && b < r->data)
r = r->left;
// IF both a and b are on the RIGHT side.
else if (a > r->data && b > r->data)
r = r->right;
}
if(a>b)
return maxElementInpath(r, a);
else
return maxElementInpath(r, b);
}

1 Comment
https://www.ritambhara.in/max-value-node-between-two-elements-of-bst/
my doubt is
/HERE getmax function is not defined /