Number of ways to arrange tiles on a board

Given a board of size 2*n and tiles of dimension 1*2 each. In how many ways can we arrange the tiles so that entire board is covered. We can only place the tiles either horizontally or vertically without breaking them.
For example, if the board is of length 3 (n=3), then tiles can be placed in following three ways:

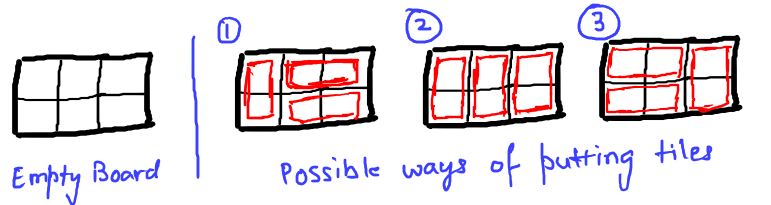
Solution:
If you do not want to read, you can watch the video below, else continue reading the post:

There is only one variable in the problem: n, i.e the length of board.
This problem can be easily solved recursively. Let us look at the ways in which the first tile can be placed. We can place the tile only in horizontal or vertical order:
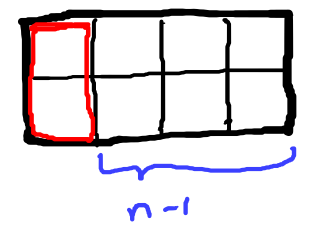
1. If the first tile is placed vertically.

The problem is now reduced to, “Find number of ways in which tiles can be placed on the board of length (n-1)”.

2. If the first tile is placed horizontally.

The second tile has to be placed in the second row horizontally, there is no way to place it vertically.

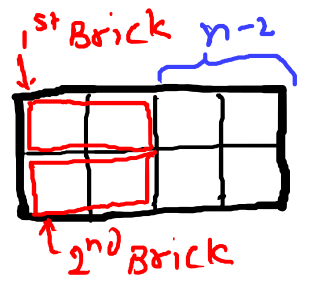
The number of ways to arrange tiles in a board of length n = number of ways to arrange tiles in a board of length (n-1) +
                                                             number of ways to arrange tiles in a board of length (n-2)

This is the same recursive equation as that of Fibonacci series. The only difference is in the terminating conditions. The two terminating conditions (for n=1, and n=2) are:
When n=1, There is only one solution, because the length is 1, then one tile can be placed only vertically

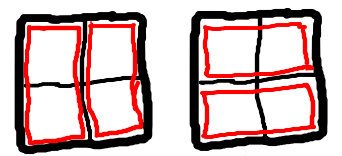
When n=2, Then there are following two ways of putting the tiles:

The fibonacci code will have a slight change in the terminating conditions as shown in the code below:

int numOfWays(int n)
{
  if(n == 1)
    return 1;
  if(n == 2)
    return 2;  // THIS IS DIFFERENT FROM FIBONACCI
  return numOfWays(n-1) + numOfWays(n-2);
}