Print all diagonals of a matrix in alternate order

Given a square matrix of order N*N, write code to print all the elements in the order of their diagonal in alternate forward and backward order.
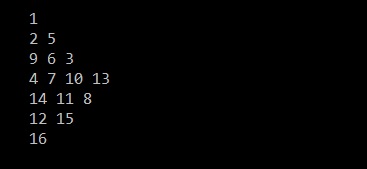
For example, in the below matrix, the elements should be printed in the marked (in red) order, and the final output should be as shown below:

Note that the diagonals are printed in alternate order.

Solution

We have already covered two questions on similar subject, one on printing both the diagonals of a matrix and other on printing all the elements of a matrix in diagonal order. This question is a modification on the second one. In fact, one of our users, Akash Tomar asked this question on our facebook page.

From the previous question, we know that there are 2*N-1 diagonals. If we can find the starting point of each of the digonal then we can move forward untill we hit the other end of the matrix. Finding first element of diagonal is easy, we just need to keep a note of the direction and use the solution of our previous post.

Below is the code:

#define N 4
void printAllDglAlt(int a[N][N])
{
    int i = 0, j = 0;
    int direction = FORWARD;
    // Loop to print each diagonal
    for (int cnt = 0; cnt<2 * N - 1; cnt++)
    {
        // Print each diagonal in new line
        cout << std::endl;
        if (cnt<N)
        {
            if (direction == FORWARD)
            {
                i = cnt;
                j = 0;
            }
            else
            {
                i = 0;
                j = cnt;
            }
        }
        else
        {
            if (direction == FORWARD)
            {
                i = N - 1;
                j = (cnt + 1) % N;
            }
            else
            {
                i = (cnt + 1) % N;
                j = N - 1;
            }
        }
        while (i >= 0 && i<N && j>=0 && j<N)
        {
            if (direction == FORWARD)
            {
                // Printing forward diagonal
                cout << " " << a[i][j];
                i--;
                j++;
            }
            else
            {
                // Printing Backward diagonal
                cout << " " << a[i][j];
                i++;
                j--;
            }
        }
        direction *= -1;
    }
}
int main()
{
    int a[N][N] = { { 1, 2, 3, 4},
                    { 5, 6, 7, 8},
                    { 9, 10, 11, 12 },
                    { 13, 14, 15, 16 }, };
    printAllDglAlt(a);
}

The output of the above code will be:

Please let us know if you have any querry/questions/suggestion. Feel free to comment.