Radix Sort

Consider an array that stores account numbers of all employees. One unique thing about account numbers is that they have equal number of digits. Let us take example where, account numbers are three digits long, and array has 6 account numbers are shown below

int arr[ ] = {582, 675, 591, 189, 900, 770}

Range of elements in this array can be from 100 to 999, but actual number of elements are very less, therefore counting sort is not a good choice. In this situation Radix sort is a good algorithm to use. Idea behind radix sort is to sort numbers on each digit one at a time starting with least significant digit using some other stable sorting method. This other stable
method is usually counting sort, because range of digits is from 0 to 9.

FOR each digit i starting from LSD to MSD
    Use counting sort to sort numbers in array on value at digit i

For the given input array, how radix sort algorithm proceed is shown in Figure below. Elements of array are shown vertically for sake of clarity.

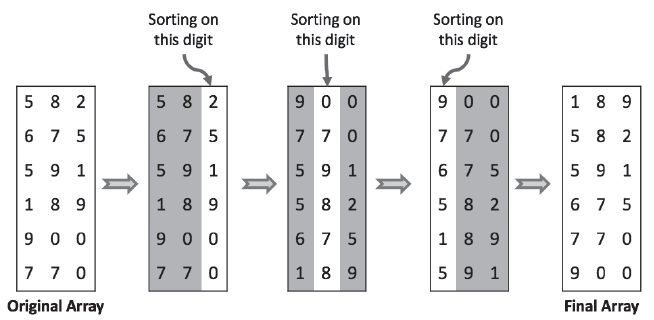
While sorting, consider only the digit that we are sorting on and not the complete number. If we are using comparison sort, then only specified digits of two numbers should be compared. For example, while sorting on least significant digit, 900 is considered less than 189 because LSD of 900 (i.e 0) is less than the LSD of 189 (i.e 9).
Radix sort actually use some other sorting algorithm to sort numbers on individual digits. So, it is always discussed with other sorting algorithm used as a sub-routing of Radix sort. Performance of radix sort depends on choice of that other algorithm.
If quick sort is used to sort individual digits, then overall time taken by radix sort is O(k.n.lg(n)) where k is number of digits in each number. Obviously, it is less optimized than quick sort itself. If we use counting sort then we can sort the numbers in O(k.n) time using O(n) extra memory. The time taken is linear when k is very small constant in comparison to n.
An important requirement of Radix sort is that the sorting method used must be stable, otherwise result of radix sort may not be correct.
To make Radix sort work, we need to modify counting sort to accept position of digit (place value) and sort numbers based on that digit. Modified counting sort function is given in this post.

// SORT THE NUMBERS BASED ON THE DIGIT AT placeValue
void countSort(int *arr, int n, int placeValue)
{
    int finalArr[n]; // FINAL OUTPUT ARRAY
    int count[10] = {0}; // MAX UNIQUE = 10
    int i;
    for (i = 0; i < n; i++)
        count[(arr[i]/placeValue)%10]++;
    for (i = 1; i < 10; i++) count[i] += count[i-1]; for (i = n - 1; i >= 0; i--)
    {
        finalArr[count[(arr[i]/placeValue)%10]-1]=arr[i];
        count[(arr[i]/placeValue)%10]--;
    }
    for (i = 0; i < n; i++)
        arr[i] = finalArr[i];
}

This modified counting sort code is used by radix sort in code below to sort array of numbers

void radixSort(int arr[ ], int n)
{
// FIND MAX NUMBER TO KNOW NUMBER OF DIGITS
int m = getMax(arr, n);
for ( int placeValue = 1; m/placeValue > 0;
placeValue *= 10)
countSort(arr, n, placeValue);
}

To learn more about searching and sorting algorithms and questions based on these algorithms buy our book:
Searching and sorting for Coding interviews.