Array of products except the current elements
January 15, 2013Non-recursive solution to tower of hanoi
January 17, 2013Tower of Hanoi code
Tower of Hanoi is a Mathematical Game. There are 3 pegs (Rods) and number of discs, each of different size, which can be inserted into the rods. All discs are initially inserted into one rod in increasing order (smallest at the top and largest disc at the bottom).
You have to move all the discs from source rod to Destination rod, with below 2 restrictions:
- Only one disc can be moved at a time.
- You cannot place a larger disc on the top of a smaller disc ever.
For example: If the Pegs are named as S, D & E (Source, Destination & Extra) and there are 4 discs, the initial state will be
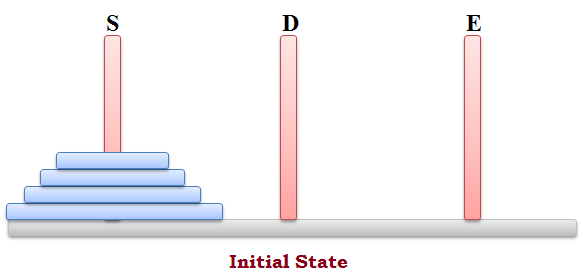
And final state will be:
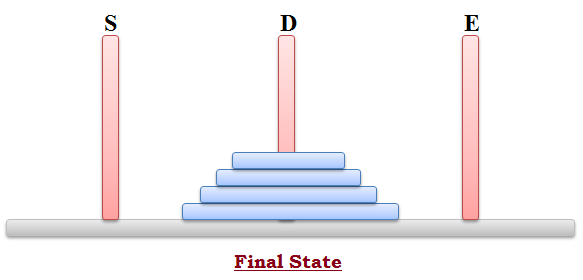
Write a function that accept the names of three rods (S, D & E) and the number of discs, and print the movement of discs between the rods such that all the rods are moved from S to D.
The signature of the function will be
/* The three char represents the characters representing three rods * and n is the number of discs (initially in s) */ void towerOfHanoi(char s, char d, char e, int n)
Solution:
The solution to this problem can be easily thought in a recursive approach. The Problem:
Move n Discs from S to D using E
Can be solved in 3 steps:
Step-1: Move n-1 discs from S to E using D Step-2: Move the nth disc from S to E Step-3: Move n-1 discs from E to D using S
If you notice, the Step-1 & Step-3 are recursive calls to the same function. Hence the code of the function will be:
void towerOfHanoi(char s, char d, char e, unsigned int n)
{
if(n > 0)
{
towerOfHanoi(s, e, d, n-1);
printf("Move Disk-%d FROM %c TO %c\n", n, s, d);
towerOfHanoi(e, d, s, n-1);
}
}
If we run this Call this function for 3 discs (n=3) like below
towerOfHanoi('s', 'd', 'e',3);
Then the output will be
Move Disk-1 FROM s TO d Move Disk-2 FROM s TO e Move Disk-1 FROM d TO e Move Disk-3 FROM s TO d Move Disk-1 FROM e TO s Move Disk-2 FROM e TO d Move Disk-1 FROM s TO d
The actual movement of the disks will be as shown below:
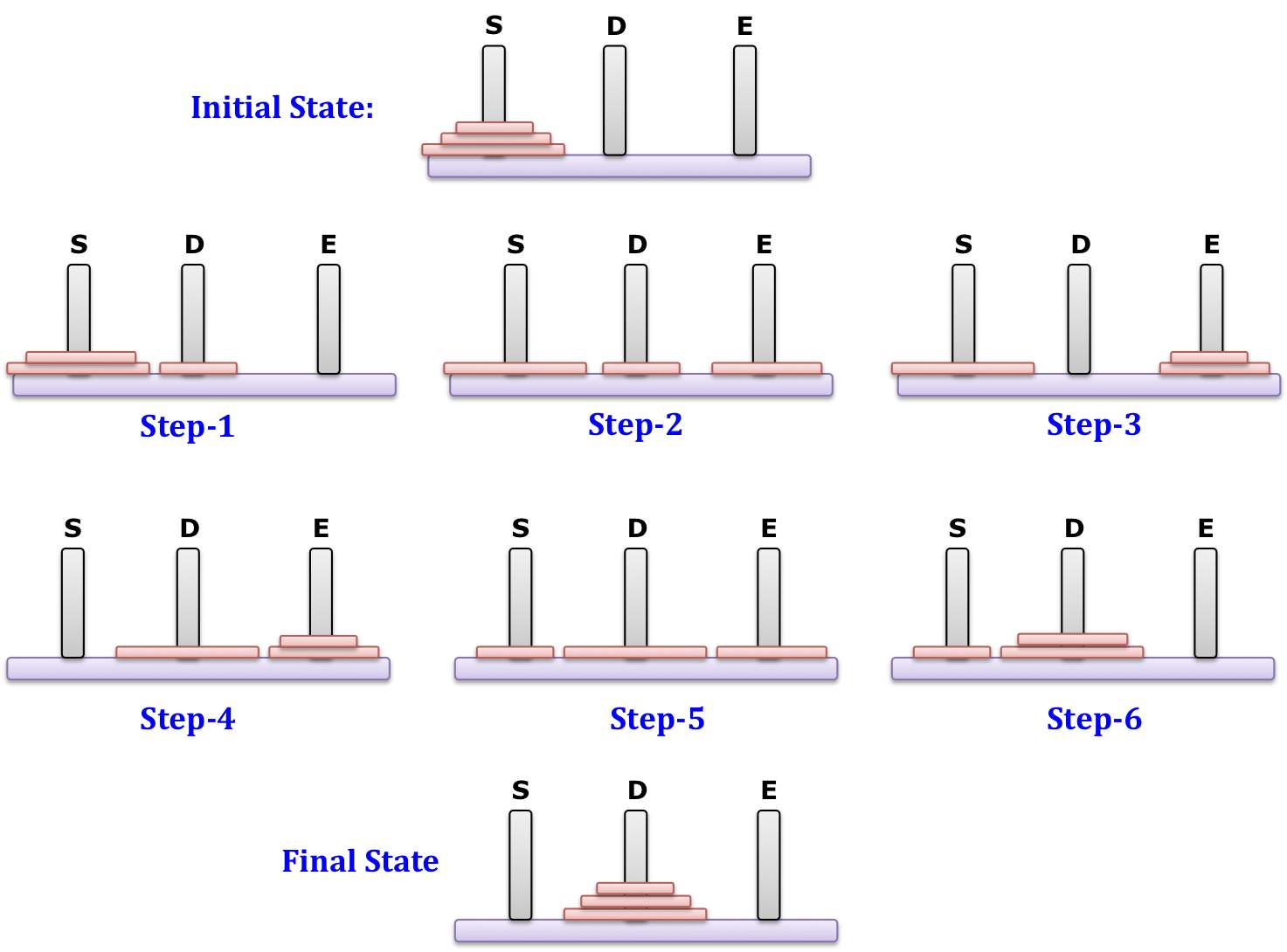
Next: Non-Recursive solution to Tower-of-hanoi

7 Comments
Arrey Rawat, regarding this “tower of Hanoi” problem ( heard this phrase for the first time)..can’t you do the following to minimize the steps:
Step 1: move the small disc from “s” to “e”
Step 2: Move medium disc from “s” to “e”
Step 3: Move large disc form “s” to d”
Step 4: move medium disc form “e” to d”
Final Step: move small disc from “e” to “d”
Thus, you accomplish in two less steps..unless I am missing something that I obviously don’t understand about computer science…??
What you are saying is absolutely correct, but this solution is for 3 disks (my example & your solution in above comment) and is more from intuitive point-of-view (human).. What if I increase the number of disks to 10, it will become difficult for humans to do it.. Problem is to generalize it (its applicable for any n-number of disks) to write an Algorithm So that computer can solve it..
Compare it with Chess program, what looks obvious to human may be very difficult for computer to infer…
The 2nd solution (https://www.ritambhara.in/non-recursive-solution-to-tower-of-hanoi/) is highly optimized and takes the least number of steps.
i cant understand this…whats the use of this
This is a typical question asked in interview (mostly at the fresher level).. plus it is one of the applications of recursion.. i.e how you can use recursion to solve otherwise complex looking problem easily
Hi
is it possible to use your figure of the different states of solving the tower of hanoi task in a book chapter I am writing? The publishers require me to contact the originator of the figure – and to check with them if the figure can be used, and also, if you agree, I will need to know who to acknowledge.
Hope this is o.k
magda
please feel free.. It will be great if you can mention the website as a source.
If there are 4 rods then what is the procedure?